Graph is everything
소셜 네트워크도 그래프다. 분자 구조도 그래프다. 넷플릭스 시청 내역도 그래프다. 주체와 관계가 있는 모든 종류의 데이터는 그래프의 꼴로 치환이 가능하다. 하여튼 아주아주 그래프가 중요하다고들 하는데 난 그래프를 잘 모른다. 전공 선택 과목이었던 조합 및 그래프 이론을 나는 왜 듣지 않았을까.
그래프를 뉴럴넷을 보기에 앞서 그래프에 대한 기본만 한 번 훝어보고자 한다. 그래프는 주체가 되는 Node와 관계를 표현한 Edge로 이루어졌다. 관계는 Directed와 Undirected 관계로 나눌 수 있다. 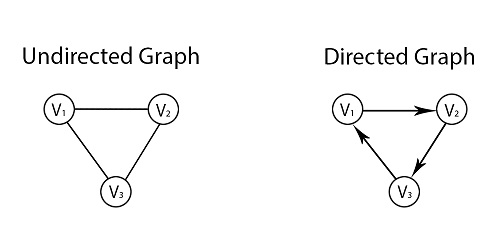
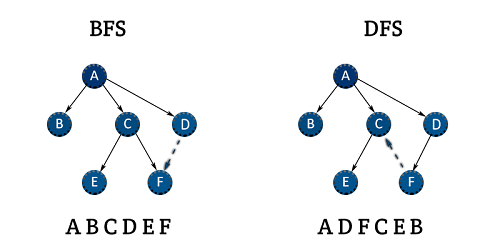
특정 노드에 붙어있는 edge의 숫자를 노드의 degree라고 표현하는데 만약 전체 데이터에서 N개의 노드가 있다면 모든 노드의 연결관계와 degree를 N x N 매트릭스로 표현할 수 있다. 표현된 매트릭스의 row sum은 해당 노드의 degree가 될 것이고, Undirected 그래프는 symmetric matrix가 될 것이다. 알고리즘과 코딩 테스트를 따로 준비해본적은 없지만 DFS, BFS에 대해서는 많이도 들어봤다. 그래프를 탐색하는 방식의 차이인데 깊게 혹은 넓게 볼 것인지의 차이라고만 이해하면 될 것 같다.
그래프에서 ML을 통해 해결하고자 Network Task는 아래와 같은데 이것들을 해결하는 일이 쉽지가 않다.
(1) Node Classification (Anomaly Detection, Fraud Detection ..)
(2) Link Prediction (Recommender System)
(3) Network Similarity
우선, 그래프 데이터는 이미지나 시계열과 같이 정형적인 형태의 데이터로 취급할 수 없다. 네트워크라는 것이 이미지와 같이 고정된 크기의 것이 아니라 Input이 가변적이고 시계열과 같이 선후관계가 있는 것이 아니라 노드들을 Ordering 하는 것이 불가능하기 때문이다. 본격적으로 GNN 모델링을 하기에 앞서 그래프 데이터를 어떻게 임베딩할 것인지에 대한 기본 개념을 하나 알고 가자.
Random Walk Embeddings
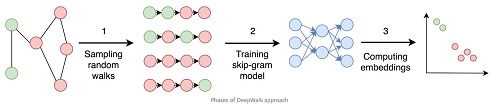
데이터의 구조와 관계를 알지 못하는 상태에서 표본적으로 형태를 구체화하기 위해 Random Walk가 수행된다. Random Walk는 아무 Node를 시작점으로 잡고 마구 움직여서 주위에 어떤 Node로 갈 수 있는지 탐색하는 기법이다. 여기서 “마구 움직임”의 전략을 DFS 혹은 BFS로 선택함에 따라 “어디까지 갈 수 있는지”와 “어디로 많이 갈 것인지”를 탐색할 수 있다. 이런 랜덤워크 프로세스를 활용하여 그래프 데이터를 임베딩하려는 시도가 DeepWalk (KDD 2014)에 있었는데
컨셉적으로 이해해보자면, 각 Node를 d 길이의 벡터로 임베딩할 것인데, Random walk를 통해 가깝다고 나타단 노드와는 inner product값이 크고, 멀리 있는 노드와는 값이 작도록 학습될 것이다. 그런데 DeepWalk에서는 Random walk를 정말로 random하게 취하여 그래프의 전체 Structure를 잘 캡쳐하지 못했었는데, 이후에 나온 node2vec (KDD 2016) 논문에서 이것을 보완하여 dfs, bfs 전략을 융합했고, 현재에도 많이 사용되고 있다고 한다.
Graph Neural Network (GNN)
N개의 노드의 skip gram loss를 최소화하는 N x d(# of feature) 매트릭스를 학습하는 임베딩 기법은 shallow encoding이라 불린다. 이런 고전의 방법들은 몇가지 한계점이 있는데
(1) 각 노드가 Parameter를 공유하지 않고
(2) 학습에서 보지 않은 노드를 임베딩할 수 없고
(3) 엣지 관계 이외의 노드의 특징을 임베딩 과정에 반영할 수 없었다.
따라서 이런 한계점들을 극복하고자 고안된 “깊은” 임베딩 기법이 바로 Graph Neural Networks이다. GNN의 가장 큰 특징은 특정 Node의 Neighbor Node 정보를 Aggregate한 값을 임베딩에 활용하는 것이라 볼 수 있는데 Aggregation에 대한 구체적인 이해를 위해 아래의 알고리즘을 천천히 봐 볼 필요가 있다.
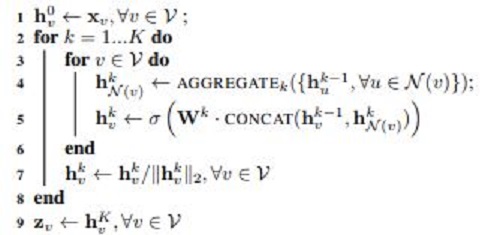
우리가 타겟하는 노드가 v일때, v에게는 N(v)라는 이웃 노드 집합이 존재한다. 4번 째 줄은 N(v)안에 있는 각각의 u 노드에 존재하는 N(u)의 정보를 취합하는 과정이며 5번 째 줄은 u노드의 정보와 N(u)의 정보를 취합하는 과정이라는 것을 알 수 있다. 0-depth node의 정보를 얻기 위해 1-depth의 정보가 들어가는데, 1-depth의 정보에는 2-depth와 3-depth의 정보가 들어가는 것이다.
정리하자면 GNN은 각 노드에 특화한 임베딩 벡터를 업데이트 하는 것이 아니라 목표 노드의 이웃을 잘 취합하도록 학습된다. 따라서 임베딩 과정에서 각 노드들이 Parameter를 공유할 수 있고 새로운 노드에도 바로 적용할 수 있다는 장점이 있다.
Node Classification Task (Example)
그래프 데이터는 일반적인 ML 공부 과정에서는 다룰 일이 없어 처음 봤을때 꽤나 낯설게 느껴질 수 있다.
Cora Dataset

2708개의 과학 논문들이 서로 어떤 관계로 cited되었고 어떤 단어가 포함됬는지에 관한 데이터 셋
content 파일은 (논문의 id) / (각 논문의 feature 정보 - 1433개의 단어) / (논문의 장르) 3종류의 정보가
cited 파일은 (참조된 논문) -> (참조한 논문) 2개의 컬럼으로 이루어져있다.
cites 데이터는 전체 그래프가 아닌 개별 edge 정보만 담고 있기 때문에 매트릭스로 가공해주자
데이터를 어떻게 가공해야하는지에 대해서는 github.com/tkipf/pygcn 를 참조했다.
1
A, features, labels, idx_train, idx_val, idx_test = load_data()
load_data 함수를 통해 데이터를 가공해서 불러오고나면 그래프 정보가 담긴 매트릭스 A를 얻을 수 있다.
label은 총 7가지로 Case_Based / Genetic_Algorithms / Neural_Networks 등등이 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class GCN_layer(nn.Module):
def __init__(self, in_features, out_features, A):
super(GCN_layer, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.A = A
self.fc = nn.Linear(in_features, out_features)
def forward(self, X):
return self.fc(torch.spmm(self.A, X)) #이웃 정보 종합
class GCN(nn.Module):
def __init__(self, num_feature, num_class, A):
super(GNN, self).__init__()
self.feature_extractor = nn.Sequential(
GNN_layer(num_feature, 16, A),
nn.ReLU(),
GNN_layer(16, num_class, A)
)
def forward(self, X):
return self.feature_extractor(X)
GNN에서 가장 기본적인 형태인 GCN(Graph Convolutional Network) 모델의 구현으로 바로 넘어가보자. GCN 모델은 2번의 GCN_layer를 넘어가게 되는데 GCN_layer함수가 의미하는 바가 무엇인지 이해해야 한다.
GCN_layer class의 forward 함수는 A와 X의 곱으로 얻어진 매트릭스를 row 단위로 fully connected layer로 넘기는 역할을 한다. A는 모든 논문의 그래프 정보가 담긴 2708 x 2708 매트릭스, X는 각 논문읜 feature 정보가 담긴 2708 x 1433 매트릭스이다. 그렇다면 AX는 다시 2708 x 1433의 매트릭스가 생성되는데 이 행렬의 각 element가 무엇을 의미하는지 생각해보자.
행렬의 (1,1)이 의미하는 것은 id 1의 논문과 연결된 모든 논문들의 feature 1 값의 곱이다. 그리고 2708 x 1433의 매트릭스가 fc layer를 거치고 나서는 2708 x 16(우리가 임의로 설정한)의 크기로 임베딩되었다. 이런 GNN_layer를 두 번 탄다는 것은 A*(embeded(AX))의 행렬을 얻는 것과 같은 소리이다.
다시 한 번 곱해진 위의 행렬의 (1,1) 값의 의미를 생각해보자.
논문1에 연결된 논문들에 연결된 논문들의 feature 정보까지도 포함되어있다는 것을 이해하자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def train(model, Loss, optimizer, num_epochs):
train_loss_arr = []
test_loss_arr = []
best_test_loss = 99999999
early_stop, early_stop_max = 0., 10.
for epoch in range(num_epochs):
# Forward Pass
model.train()
output = model(features)
train_loss = criterion(output[idx_train], labels[idx_train])
# Backward and optimize
train_loss.backward()
optimizer.step()
train_loss_arr.append(train_loss.data)
if epoch % 10 == 0:
model.eval()
output = model(features)
val_loss = criterion(output[idx_val], labels[idx_val])
test_loss = criterion(output[idx_test], labels[idx_test])
val_acc = accuracy(output[idx_val], labels[idx_val])
test_acc = accuracy(output[idx_test], labels[idx_test])
test_loss_arr.append(test_loss)
if best_ACC < val_acc:
best_ACC = val_acc
early_stop = 0
final_ACC = test_acc
print('Epoch [{}/{}], Train Loss: {:.4f}, Test Loss: {:.4f}, Test ACC: {:.4f} *'.format(epoch, 100, train_loss.data, test_loss, test_acc))
else:
early_stop += 1
print('Epoch [{}/{}], Train Loss: {:.4f}, Test Loss: {:.4f}, Test ACC: {:.4f}'.format(epoch, 100, train_loss.data, test_loss, test_acc))
if early_stop >= early_stop_max:
break
print("Final Accuracy::", final_ACC)
방금 생성한 GCN 모델과 비교의 대상이 될 base FC 모델을 같은 방법으로 학습할 것이다.
아래는 가장 기본적인 Fully Connected Nueral Network 이다.
1
2
3
4
5
6
7
8
9
10
11
12
class FCN(nn.Module):
def __init__(self, num_feature, num_class):
super(FCN, self).__init__()
self.feature_extractor = nn.Sequential(
nn.Linear(num_feature, 16),
nn.ReLU(),
nn.Linear(16, num_class)
)
def forward(self, x):
return self.feature_extractor(x)
이제 모델을 할당하고 학습을 시작한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# FCN 학습 돌려서 epoch에 따른 Loss 확인
model = FCN(features.size(1) , labels.unique().size(0))
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.1, weight_decay=0.0001)
train(model, criterion, optimizer, 1000)
# GCN 학습 돌려서 epoch에 따른 Loss 확인
model = GCN(features.size(1) , labels.unique().size(0), A)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.1, weight_decay=0.0001)
train(model, criterion, optimizer, 1000)
FCN을 통한 최종 ACC는 0.5770 GCN을 통한 최종 ACC는 0.8280으로 나타났다.
사실 직관적으로도 GCN의 성능이 더 우수할 것 같다. FCN이 분류에 활용할 수 있는 정보는 해당 논문의 단어 데이터 밖에 없는데 GCN은 연결된 다른 논문의 정보도 활용하기 때문이다. 그래프 뉴럴 넷의 가장 기본적인 컨셉과 모델링을 실습했다.
끝