Histogram Loss도 그렇지만 최근의 연구들에서 범용적으로 사용되던 quadratic loss의 한계점을 지적하는 경우가 많은 것 같다. 해당 논문은 기존 로스의 한계점을 꽤 논리적으로 분석했고 그럴듯한 대안을 제시한다. 저자가 수학적 조예가 깊은 사람이라 읽는데 조금 어려움은 있었지만 접근법과 성능면에서 분명 읽을 가치가 있는 논문이라 생각한다. 여기서 제안된 Extreme Valuee Loss는 risk management 분야에서 자주 등장하는 EVT(extreme value theorem)에 기초하고 있다. 따라서 논문을 읽기 앞서 GRU(gate recurrent unit), EVT, Binary Cross Entropy의 개념을 보고 온다면 좋을 것 같다.
Paper Summary
Contribution 01.
Formal analysis on why deep neural network suffers extreme problems
during predicting time series data with extreme value
Contribution 02.
Propose a novel loss function called Extreme Value Loss (EVL) based on extreme value theory
Contribution 03.
Propose a brand-new Memory Network based neural architecture to memorize extreme events in history
Preliminaries
Time Series Prediction
Optimization Goal: 과거 1d 정보를 인풋으로 실제와 예측의 차이를 최소화하도록 모델을 학습
Quadratic loss를 최소화하는 것을 기본으로 많은 모델이 등장했고
최근에는 LSTM에서 forget term을 추가한 GRU가 많이 쓰이고 있다.
Extreme Events
실제 값을 기준으로하여 +/- 방향으로 임의의 threshold를 설정하고 {-1,0,1}로 발생 여부를 분류한다.
Heavy-Tail Distribution
극값을 가질 확률이 큰 분포, 범용적으로 사용되는 Gaussian / Poisson 분포는 light-tail Distribution
light - tail 형태를 가정하고 모델을 학습하면 평균은 잘 맞출지 몰라도 꼬리 부분의 정보를 손실하게 된다.
EVT (Extreme Value Theory)
EVT studies the distribution of maximum in observed sample
Maximum of Random Variable의 분포를 추정하는 것을 목적으로 한다.
간단히 생각해서 정규 분포의 꼬리 부분을 뚝 자른 후, 잘라진 부분의 분포를 추정하는 것이라 볼 수 있다.
Maximum distribution의 y를 추정하는 방식은 (1) Block maxima (2) Peaks over threshold 두 가지로 나눌 수 있는데 각 방식에 따라 Generalized된 확률변수의 값이 조금 달라지게 된다. 해당 논문에서는 (1)의 방식을 택했고 아래와 같다.

여기서 분포의 형태를 결정하는 감마는 하이퍼 파라미터로 모델의 학습 과정에서 우리가 결정해주면 된다. 확률 변수를 정의하고 선형 변환을 통해 분포를 추정하는 과정은 고민하지 않는 것이 정신 건강에 좋다. 눈으로 보면 아래와 같다.
Modeling the tail
일반화한 분포를 사용하여 Extreme Event가 발생할 수 있는 확률에 대한 모델링이 가능하다.
아래의 크사이도 역시 하이퍼 파라미터로 이상치라 판단할 수 있는 임계값이라 볼 수 있다.

Empirical Distribution After Optimization
최적화의 목적함수인 minimizing quadratic loss는 x에 대한 y의 조건부 확률의 likelihood를 maximize하는 것과 동치이다. 따라서 문제를 sample에 대한 조건부 확률값을 모두 곱한 것을 최대화하는 것으로 치환하고 나면 이것이 non parametric Gaussian Kerenl을 통해 KDE를 수행하는 것과 같다고 한다. (그냥 납득하고 넘어가자 자세한 설명이 없다) 이것은 Extreme Modeling을 수행하는데 많은 제약을 갖게 만든다고 저자는 말한다. 그리고 이제서야 본론으로 넘어갈 수 있다.
Why Deep NN could suffer Extreme Event Problem
Since nonparametric kernel density estimator only works well with sufficient samples
the performance therefore is expected to decrease at the tail part of the data

Extreme Event Problem은 모델이 극단값에 대해 과적합하거나 아예 학습하지 못하는 문제를 말한다.
Underfitting Problem:
극단값을 학습하지 못해 예측값이 평균 근처에서 맴도는 현상Overfitting Problem:
극단값을 너무 민감하게 받아들여서 시도때도 없이 극한값이라고 예측해버리는 현상
두 가지 문제 모두 치명적이라고 볼 수 있는데 딥러닝 모델이 위의 문제들을 겪을 수 밖에 없는 이유를 살펴보자. 앞서, quadratic loss를 통해 모델링을 하는 것은 Gaussian 분포를 가정하고 최적화되는 것이라 말했다. 그렇다면 예를 들어 두 샘플 x1, x2의 실제값이 1과 2이고 우리가 설정한 Extreme Value가 2 이상의 값이라면 어떻게 될까. 모델을 최적화함에 있어 극단값의 정보가 반영되지 않았고 모델은 실제의 분포보다 light - tail의 정규분포를 출력할 것이다.

이것을 위와 같이 표현할 수 있고, 같은 방법으로 x2에 대한 y2의 확률값을 추정하면 true Value보다 작은 값을 출력할 것이다. 그 말은 즉, 2보다 큰 y 값들에 대해서는 실제의 값보다 더 작은 값을 추정한다는 것이다. Underfitting problem이라는 뜻이다.
앞선 연구들은 극단값들을 모델에 반복적으로 학습시켜 문제를 해결하고자 했는데 적절한 수치를 넘겨버리면 바로 Overfitting Problem이 발생해버렸다. 적절한 가중을 가해 Extreme Event Problem을 해소하면서도 성능 좋은 예측 모델을 만들 수 있는 방법이 논문에 제안되었다.
핵심적인 아이디어는 두 가지다.
Memorizing Extrem Events
Use memory network to memorize the characteristic of extreme events in history
Modeling Tail Distribution
Approximated tailed distribution on observations and provide a novel classification called Extreme Value Loss
Network Structure
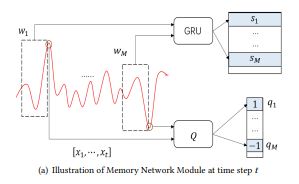
Memory Network Module
과거의 시계열 정보, 특히 이벤트의 발생을 잘 기억하도록 학습되고 활용되는 부분이다. 전체 시계열 구간에서 w 사이즈의 윈도우를 랜덤하게 M개 추출하고 각 윈도우를 잘 임베딩 할 수 있는 GRU 모듈을 학습한다. 잘 임베딩 된다는 것은, latent vector S에 이벤트 발생을 분류할 수 있는 정보가 잘 녹아들었다는 것을 의미한다. 잘 임베딩 된 어떤 벡터가 이벤트가 발생하는 특성을 잘 포함하고 있을 때, 새로 들어온 어떤 인풋이 해당 벡터와 굉장히 유사하다면, 우리는 아웃풋 역시 이벤트가 될 것이라 추측할 것이다.
구체적인 목적함수와 학습의 선후관계는 나중에 다시보도록 하자.
Attention Mechanism and prediction
w 사이즈의 1d 시계열 데이터를 받아 t+1 시점의 값을 GRU 유닛을 통해 예측하는 부분은 기존 다른 연구의 것들과 동일하다. 여기서 저자가 제안한 부분은 앞서 Memory Network Module에서 학습한 정보를 Attention으로 활용하여 예측값에 반영하는 것이다.

Attention의 가중치 C는 H와 S의 inner product 값이다. 여기서 H는 새로운 input window를 GRU로 임베딩한 벡터이고 S는 앞서 랜덤 샘플한 M개 구간을 임베딩한 벡터들이다. Inner product 알파에 곱해지는 Q는 M개 구간의 이벤트 발생 여부이다. 정리하자면 유사한 과거 시계열 구간들에 + 방향의 이벤트 발생이 많았다면 기존 예측값보다 큰 값을, 반대의 경우에는 기존 예측값보다 작은 값을 최종 Output으로 삼을 것이다.
구체적인 알고리즘을 확인하기 전에 목적함수가 되는 Loss를 살펴보도록 하자.
Extreme Value Loss
문제를 간단히 하기 위해 Event는 (+) 방향으로만 발생한다고 생각해보자. 그럼 t+1 시점에 이벤트가 발생한다면 Label: 1, threshold를 넘지 않았다면 Label: 0 이 된다. 그렇다면 Task는 이제 binary classfication이 되는 것이고 우리는 널리 알려진 binary cross entropy loss를 쓸 수 있다. EVL은 Binary CE Loss에 ‘적절한’ 가중치를 부여한 방식이라고 볼 수 있다. 그리고 EVL의 가중치는 논문의 앞부분에 언급된 Generalized Extreme Value distribution을 사용한다.
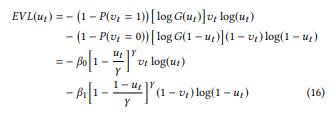
한줄 한줄이 어떤 의미를 갖는지 해석하고자 하면 너무 피곤해진다. EVL은 기본적으로 CE와 같은 컨셉을 공유한다. 0을 1이라 예측하면 Loss가 올라간다. 1을 0으로 예측하면 Loss가 올라간다. 그런데 기존에 CE는 두 가지의 잘못된 예측에 동일한 크기의 Loss가 부여됬다면 EVL은 1을 0으로 예측한거에 더 큰 Loss가 부여된다. 그 이유는 맨 윗 줄의 (1 - P(v == 1)) = 정상일 확률이 (1 - P(v == 0)) = 이벤트일 확률보다 훨씬 크기 때문이다. 결국 EVL의 컨셉은 과거의 연구들이 Underfitting Problem을 해소하고자 반복적으로 Extreme Value를 학습한 것과 동일하다. 다른 점은 임의의 계수를 주관적으로 설정하여 가중하는 것이 아니라 heavy - tail로 선형 변환된 Sample의 분포를 사용한다는 것
Optimization

무책임하게 알고리즘을 던져 놓고 리뷰를 마무리하고 싶다.
우선 한줄한줄 내려가기 전에 학습에 사용 되는 두 가지 로스를 알아보자.


보다시피 L2 로스는 EVL만, L1로스는 EVL에 quadratic loss를 함께 사용하는 로스이다. 로스가 알고리즘의 어디에 있는지 살펴보면 L2로스는 Memorize Network Module에, L1로스는 최종 아웃풋을 예측하는데 사용된다. 기억해보자면 L2 로스는 단순히 CE의 변형일 뿐이다. 그렇다는 것은 분류 문제를 위해 사용된다는 것이다. 이벤트 분류에만 사용되는 것이다.
전체 1d 시계열에 대해 w사이즈의 M개 구간을 임의로 샘플링한다.
각 샘플은 j ~ j + w 구간을 의미하고 우리의 학습 라벨은 j + w + 1 시점의 이벤트 발생 여부이다.
유사도 계산에 사용될 Vector S는 이벤트 발생 여부를 잘 분류하도록 학습된 GRU의 마지막 layer이다.
첫 번째 Loop를 통해 얻는 것은 분류를 잘하도록 학습된 GRU와
(이벤트 여부, Latent vector)가 들어있는 M 길이의 벡터이다.
L2 로스를 통해 학습되는 것은 Input을 잘 임베딩하기 위해 존재하는 GRU와 임베딩 정보를 통해 잘 분류해내는 행렬이다. L1 로스를 통해 학습되는 것도 크게 다르지 않다. 마찬가지로 잘 임베딩하기 위해 존재하는 GRU가 학습된다. 또한 L1을 통해서는 input과 M개 구간의 중요도를 학습하는 Attention 계수와 예측을 잘 해내기 위한 행렬이 최적화된다.
너무 다양한 파라미터들이 학습되서 처음에는 조금 헷갈리는 부분이 있을 수 있지만 학습의 순서만 납득한다면 이해할 수 있다. 마지막으로 명심해야할 것은, 예측에 사용되는 GRU와 분류에 사용되는 GRU가 동일하다는 것. 즉 우리는 학습을 통해 w길이의 input을 GRU가 분류와 예측 모두에 최적화된 Vector로 임베딩하기를 기대하는 것이다.
Experiments
물론 논문의 실험을 맹신할 수는 없지만 논문의 전개가 타당했다고 느껴졌기 때문에 압도적인 성능 향상에도 신뢰가 간다.
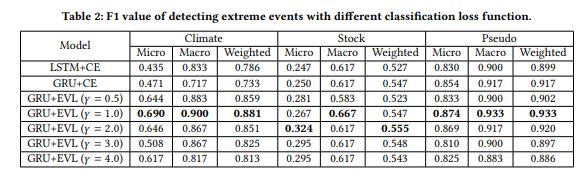
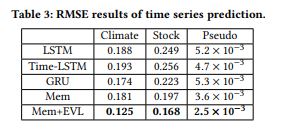
위의 표는 해당 모델이 이벤트를 분류함에 있어 얼마나 우수한지, 아래는 모델이 얼마나 잘 예측하는가에 대한 것이다. 왼쪽의 표를 보면 감마 값을 하이퍼 파라미터로 설정할 수 있음을 볼 수 있는데 EVT에 따라 감마가 커진다는 것은 분포의 tail이 점점 heavy 해짐을 의미한다는 것이다. 저자는 real world 데이터라고 볼 수 있는 stock 데이터에서 감마 2가 제일 성능이 좋으니 이것을 스탠다드로 할 것이라 말한다.
결론
데이터의 불균형은 정규 분포를 근사하는 기존 모델에 치명적임을 논리적으로 잘 지적했고 과거 시계열 정보를 Attention 모듈을 통해 가중한다는 컨셉이 재밌었다. 구체적으로 어떻게 해야할지는 모르겠지만 임베딩한 M 개의 Latent Vector와의 유사함 뿐 아니라 M개 벡터간의 유사함, M개 벡터의 Temporal한 관계를 학습에 반영할 수 있는 방법은 없을까라는 생각이 든다.