지난 번 봤던 Deep Divergence Graph Kernal 논문에서 여러 번 등장했던 WL-kernel에 대해 간략히 살펴보려 한다. 사실 아주 진지한 얼굴로 논문을 펼쳤으나 엄숙한 definition과 theorem 들이 나열된 것을 보고 컨셉만 보는 것으로 컨셉을 바꾸었다.
사실 그래프 커널에 대해 깊게 공부해 보는 것이 꺼려진 이유도 위와 같은데. Graph kernel의 목적이 두 그래프의 isomorphism을 찾는 Task. 즉 깊은 위상 수학의 개념들을 요구할 것이라는 막연한 두려움 때문이었는데.. 일단 봐보도록 한다.
Weisfeiler - Lehman Test
그래프 커널의 종류에는 walk based kernel / optimal assignment kernel / subtree kernel 등등 참 여러 종류가 있는 것 같다. 오늘은 그 중 DDGK에서 주요 실험 비교군으로 삼았던 WL - kernel을 보려고 한다. 비교적 최근(2011)에 등장한 해당 기법은 WL - test of isomorphism algorithm에 기초하고 있다하니 그거부터 살펴보자. 
자. 첫 줄부터 심각한 노테이션이지만 Multiset-label M이 의미하는 바를 먼저 이해해보자. 우선 Isomorphism을 비교하려는 두 그래프는 같은 노드 라벨을 공유한다는 전제에서 시작한다. 각 노드에 1 , 2 ,3 중 하나의 라벨이 존재한다고 생각해보자. 노드에 연결된 엣지의 개수에 따라 특정 노드가 가질 수 있는 연결 정보는 다양해진다. 하나의 엣지만 존재하는 경우에는 1 -> 2, 2 -> 3 의 연결 관계를 가질 수 있고, 두개의 엣지가 존재하는 경우(두 개의 노드로 이동 경로가 존재하는 경우)에는 1 -> 2,3, 2 -> 2,3 등의 정보가 있는 것이다. 그럼 이런 연결 관계 자체를 노드의 새로운 라벨로 정의한다.
사실 내가 썼지만 이렇게 글로만 봐서는 연결 정보를 새로운 노드로 정의한다는 M의 개념이 절대 이해되지 않을 것이다. 따라서 NAVER D2에서 그림으로 잘 설명해주신 링크를 보고 이해하자.
즉, 연결관계를 새로운 라벨로 정의하고 나면 구조는 바뀌지 않은 채로 노드의 라벨만 바뀐 꼴이 되는데, 이 때 하나의 그래프에는 있는 라벨이 다른 레벨에는 없다면 두 그래프는 isomorphic 하지 않은 것이다. 그리고 이런 과정을 두 번 반복하면 그래프의 2-hob 까지의 연결 관계를 노드화하여 비교할 수 있다. 따라서 WL-Test는 사전에 정의한 n-hob의 연결 관계를 노드화하였을 때, 두 그래프의 label-set이 동일한가를 통해 Isomorphism을 확인하는 테스트라고 요약할 수 있다.
Weisfeiler - Lehman Kernels
커널에 s가 붙은 이유는 augment하는 주체에 따라 커널의 형태를 다양화할 수 있기 때문이다. 해당 논문에서는 sub-graph / edge / shortest path를 적용한 세 가지의 WL Kernel을 제시한다.
WL Kernel Framework
Definition 1에서 height가 뜻하는 것은 새로운 라벨링을 몇 번 이나 반복했는가를 뜻한다. 그리고 WL - sequence는 연결 관계를 포함하지 않은 라벨인 G(0) 부터 시작하여 n - hob의 연결관계까지를 포함한 G(n) 까지의 기록들을 순서에 따라 나열해 놓은 정보라고 볼 수 있다.

이것은 그냥 새로운 노테이션에 대한 정의일 뿐이다. k가 임의의 어떤 커널일 때, 그래프 G와 G’을 각 sequence의 위치에 따라 매치하여 커널을 통해 isomorphic을 검증한다.
Theorem 1,2 는 어디가고 바로 3인지는 모르겠지만.. 우선 positive-definite kernel정의를 보고 오자. 적용하고자하는 어떤 커널이 positive - semidifinite 하다는 것은 해당 커널 매트릭스가 symmetric & hermitian 하다는 것을 뜻한다. 또한 <G,G’>이 의미하는 Kernel Calculation은 커널을 통해 맵핑된 피쳐 스페이스에서의 inner - product를 뜻한다. 즉 theorem 3은 적용하는 커널이 positive-definite 할 때, definition 2에서 정의한 WL - sequence의 kerenl calculation의 합 역시 positive -definite kernel임을 의미한다.
WL - subtree kernel
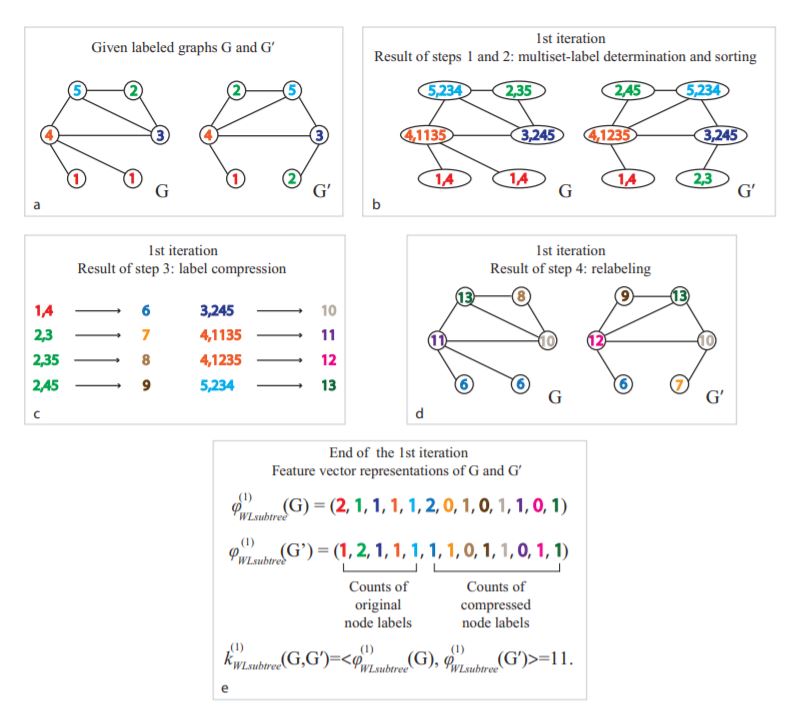
Subtree kenrel은 간단히 생각하여 노드의 빈도 비교라고 볼 수 있다. 여기서의 커널 c는 추측하건데 그냥 count의 약자가 아닐까(?) 싶다. 아래의 그림을 보는 것이 좀 더 명확하다.
(작성 중 …?)