Model Agnostic Meta-Learning (Pytorch)

다양한 태스크를 일반화할 수 있는 궁극의 모델 하나를 준비해놓고, 주어진 태스크에 소수의 횟수만으로 적합하여 과제를 수행하는 MAML(Model Agnostic Meta-Learning) 논문을 이전에 소개했다. 요번에는 실제로 MAML이 Pytorch의 문법으로 어떻게 구현되는지 구체적으로 살펴보고 Multiple Time Series Prediction Task에 적용해본다.

vmikuik의 깃헙을 참조하여 작성하였습니다.

Recap: MAML

The process of training a model’s parameters such that a few gradient steps, or even a single gradient step, can produce good results on a new task can be viewed from a feature learning standpoint as building an internal representation that is broadly suitable for many tasks

MAML의 직관적인 컨셉은 이렇다. 주어진 모든 태스크의 전반적인 특징을 관통할 수 있는 공간 중에서, 하나의 태스크가 주어졌을 때 가장 유연하게 이동할 수 있는 위치에 parameter들을 세팅해 놓겠다. 어떤 학습 전략으로? 지금 당장의 업데이트로 로스를 최소화할 수 있는 위치가 아니라, 여러 번의 업데이트가 진행됬을 때 로스가 최소화 될 수 있는 위치로, 당장의 업데이트를 수행한다.

Pytorch: MAML

생각보다 MAML을 구현하는 것이 뚝딱 간단하지가 않다. 알고리즘의 각 요소들을 모듈화해서 확인한다.

class MAML_Layer(nn.Module):
    def __init__(self, in_features, out_features):
        super(MAML_Layer, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.fc = nn.Sequential(OrderedDict([
            ('l1', nn.Linear(in_features,10)),
            ('relu1', nn.ReLU()),
            ('l2', nn.Linear(10,10)),
            ('relu2', nn.ReLU()),
            ('l3', nn.Linear(10,out_features))
        ]))
        
    def forward(self, x):
        return self.fc(x)
    
    def parameterised(self, x, weights):
        x = nn.functional.linear(x, weights[0], weights[1])
        x = nn.functional.relu(x)
        x = nn.functional.linear(x, weights[2], weights[3])
        x = nn.functional.relu(x)
        x = nn.functional.linear(x, weights[4], weights[5])
        return x

class MAML():    
    def __init__(self, 
                 model, 
                 train_tasks,
                 test_tasks,
                 inner_lr, 
                 meta_lr, 
                 K = 100,
                 inner_steps=1, 
                 tasks_per_meta_batch=1000):
        
        # important objects
        self.train_tasks = train_tasks
        self.test_tasks = test_tasks
        self.model = model
        # the maml weights we will be meta-optimising
        self.weights = list(model.parameters()) 
        
        self.criterion = nn.MSELoss()
        self.meta_optimiser = torch.optim.Adam(self.weights, meta_lr)
        
        # hyperparameters
        self.inner_lr = inner_lr
        self.meta_lr = meta_lr
        self.K = K
        self.inner_steps = inner_steps
        self.tasks_per_meta_batch = tasks_per_meta_batch 
        
        # metrics
        self.plot_every = 1
        self.print_every = 1
        self.train_losses = []
        self.test_losses = []
    
    def inner_loop(self, task):
        # reset inner model to current maml weights
        temp_weights = [w.clone() for w in self.weights]
        
        # perform training on data sampled from task
        X = torch.stack([b[0] for a in task for b in a])
        y = torch.stack([b[1] for a in task for b in a])
        for step in range(self.inner_steps):
            loss = self.criterion(self.model.parameterised(X, temp_weights), y) / len(y)
            
            # compute grad and update inner loop weights
            grad = torch.autograd.grad(loss, temp_weights)
            temp_weights = [w - self.inner_lr * g for w, g in zip(temp_weights, grad)]
        
        # sample new data for meta-update and compute loss
        loss = self.criterion(self.model.parameterised(X, temp_weights), y) / len(y)
        return loss
    
    def main_loop(self, num_iterations):
        epoch_loss = 0
        
        for iteration in range(1, num_iterations+1):
            
            # compute meta loss
            train_loss = 0
            test_loss = 0
            
            train = [self.train_tasks[i] for i in self.train_tasks.keys()]
            train_loss += self.inner_loop(train)
            
            test = [self.test_tasks[i] for i in self.test_tasks.keys()]
            test_loss += self.inner_loop(test)
            
            # compute meta gradient of loss with respect to maml weights
            meta_grads = torch.autograd.grad(train_loss, self.weights)
            
            # assign meta gradient to weights and take optimisation step
            for w, g in zip(self.weights, meta_grads):
                w.grad = g
            self.meta_optimiser.step()
            
            # log metrics
            if iteration % 10 == 1:
              print('Epoch [{}/{}], Train Loss: {:.4f}, Test Loss: {:.4f}'.format(iteration, num_iterations, train_loss.item(), test_loss.item()))
              
            self.train_losses.append(train_loss.item())
            self.test_losses.append(test_loss.item())
            
        print('Epoch [{}/{}], Train Loss: {:.4f}, Test Loss: {:.4f}'.format(iteration, num_iterations, train_loss.item(), test_loss.item()))
        

• MAML_Layer
  • 우선은 복잡하지 않게 단순한 구조의 MLP 형태를 취한다.
  • model.parameterised()
    • 원래의 모델은 건드리지 않고 업데이트 버젼의 weight를 사용하기 위한 모듈
    • 업데이트 버젼으로 로스를 구하고, 얻어진 로스로 원래 모델을 업데이트 할 것이다.

• MAML
• inner_loop
  • 여러번의 업데이트로 얻어진 weight로 얻어진 로스를 얻기 위한 내부의 loop
  • 업데이트를 몇 번 취할지는 자유로울 수 있으나 위의 구현에서는 1번만 수행하도록 제한

• inner_lr / meta_lr

  • MAML에는 기존 모델을 업데이트하기 위한 meta_learning_rate와

    inner_loop 내에서 사용할 inner_learning_rate를 구분하여 사용한다.

Train: MAML

우선 학습의 목적이 될 시계열 데이터를 가져오자. 특정 모바일 게임 유저들의 재화 획득 횟수 평균에 대한 시계열을 불러와서 (input,output) : (window 30, 1) 형태로 가공한다. 약 100일치 이상의 데이터를 window 크기로 가공하여 총 약 53만개의 학습 데이터를 생성할 수 있다.

def tensor_generator(d):
  d = d.reset_index(drop = True)
  return [
    [
      torch.tensor(d.realValue.iloc[i:i+window].tolist(), dtype = torch.float).view(-1),
      torch.tensor(d.realValue.iloc[i+window], dtype = torch.float).view(-1)
    ] 
    for i in range(len(d)-window)
    if d.realValue.iloc[i+window] 
  ]

window = 30  
# data: 80일치의 시계열 5천개
tasks = data.groupby('id').apply(tensor_generator)

index = sample(list(tasks.keys()),3000)
train_tasks = tasks[index] 
test_tasks  = tasks.drop(index)

maml = MAML(MAML_Layer(window,1), train_tasks, test_tasks, inner_lr=0.01, meta_lr=0.001)
maml.main_loop(num_iterations=500)

한 번의 epoch이 사실상 한번이 아니기 때문에 생각했던 것 보다 시간이 더 걸린다.

파란색이 Train

음 뭔가 좀 멍청한 것 같지만 일단은 목표하는 바가 few shot optimization에 있기 때문에 당장의 성능에는 큰 관심이 없다. MAML에게 기대하는 Few - Shot Learning을 얼만큼 잘 수행할 수 있는지 확인해보자.

Test: MAML

MAML의 학습 전략이 통했다는 것은, 학습된 모델이 새로운 Task에 대하여 적은 횟수의 업데이트 만으로 최적화가 가능하다는 것을 의미한다. 최적화 여부에 대한 비교 대상이 필요하기 때문에 같은 Task를 같은 구조로 같은 횟수만큼 업데이트 한 pre - trained 모델을 생성한다.

def preTrain(iteration,in_features,out_features):
    model = nn.Sequential(OrderedDict([
            ('l1', nn.Linear(in_features,10)),
            ('relu1', nn.ReLU()),
            ('l2', nn.Linear(10,10)),
            ('relu2', nn.ReLU()),
            ('l3', nn.Linear(10,out_features))
        ]))
    optimiser = torch.optim.Adam(model.parameters(), lr=0.01)
    criterion = nn.MSELoss()
    
    # fit the model
    task = [tasks[i] for i in tasks.keys()]
    X = torch.stack([b[0] for a in task for b in a])
    y = torch.stack([b[1] for a in task for b in a])
    for i in range(iteration):
      
        model.zero_grad()
        loss = criterion(model(X), y) / len(y)
        loss.backward()
        optimiser.step()
        
    return model
  
pretrained = preTrain(500,window,1)

그러면 이제 일반적으로 학습한 pretrained와 Meta Learning의 전략으로 학습한 maml이 새로 들어오는 Task에 대해서 얼마나 민감하게 반응하는지 비교해보자.

def loss_on_new_task(initial_model,task,num_steps,K,in_features,out_features,optim=torch.optim.SGD):
    
    # copy MAML model into a new object to preserve MAML weights during training
    model = nn.Sequential(OrderedDict([
        ('l1', nn.Linear(in_features,10)),
        ('relu1', nn.ReLU()),
        ('l2', nn.Linear(10,10)),
        ('relu2', nn.ReLU()),
        ('l3', nn.Linear(10,out_features))
    ]))
    model.load_state_dict(initial_model.state_dict())
    criterion = nn.MSELoss()
    optimiser = optim(model.parameters(), 0.01)

    # train model on a random task
    losses = []
    X = torch.stack([task[-(1+i)][0] for i in range(K)])
    y = torch.stack([task[-(1+i)][1] for i in range(K)])
    for step in range(1, num_steps+1):
        
        loss = criterion(model(X), y)
        losses.append(loss.item())

        # compute grad and update inner loop weights
        model.zero_grad()
        loss.backward()
        optimiser.step()
        
    return losses


maml_losses = []
pretrain_losses = []

task = [tasks[x] for x in sample(list(tasks.keys()),1000)]

for idx in range(1000):
  maml_losses.append(loss_on_new_task(
    initial_model = maml.model.fc,
    task = task[idx], 
    num_steps = 10, 
    K = 10, 
    in_features = 30, 
    out_features = 1))
  pretrain_losses.append(loss_on_new_task(pretrained,task[idx], 10, 10, 30, 1))

전체 시계열 중에 1000개를 뽑아서 각 태스크를 10번 씩 최적화 시켜준다.

def sum_calc(loss):
  res = []
  for i in range(10):
    res_i = []
    for j in range(len(loss)):
      res_i.append(loss[j][i])
    res.append(np.mean(res_i))
  return res

maml_loss = sum_calc(maml_losses) 
pretrain_loss = sum_calc(pretrain_losses)

plt.plot(maml_loss, label='maml')
plt.plot(pretrain_loss, label='pretrained')
plt.legend()
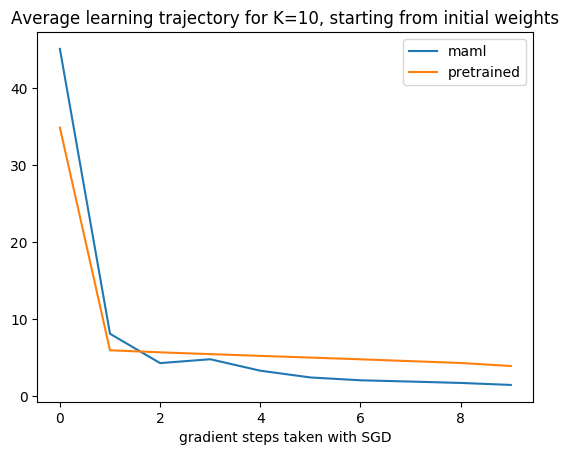
plt.title("Average learning trajectory for K=10, starting from initial weights")
plt.xlabel("gradient steps taken with SGD")
display(plt.show())

각 최적화 횟수에 따라 시계열 예측 성능이 얼마나 감소하는지 시각적으로 확인하다.

시계열 예측이라는 Task가 너무 쉬운 탓일까? Pre train 모델도 적은 횟수로 충분히 빨리 최적화되는 것 같다. 음.. 원하던 모습은 아니지만 일단 10번 업데이트 했을 때의 성능이 maml이 더 좋다고 얼머부리며 대충 넘어간다. 그럼 이어서 전체적인 로스가 아니라 실제로 개별 시계열에 대한 업데이트 과정을 하나씩 뜯어본다. 적은 횟수의 업데이트를 통해 시계열의 seasonality / change point / trend 등을 반영할 수 있을까?