grpah2vec (MLG 2017)

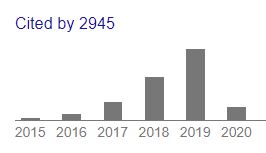
DeepWalk (KDD 2014)는 오늘을 기준으로 2945회 cited 되었는데 그 중 1300회 이상이 작년 한 해동안 쌓인 숫자이다. 그만큼 딥러닝과 그래프 분야의 논문들이 쏟아져 나오고 있다는 말이겠다. 딥워크 뿐 아니라 교과서처럼 읽히는 4~5년전 논문들에 대한 cited가 가파르게 오르고 있는데 시장의 파이도 그만큼 커졌을까?

graph2vec (MLG 2017)

오늘도 또 그래프를 본다. 그런데 요번에는 노드를 보려는게 아니라 그래프를 보려고 한다. 여지껏 구현하고 리뷰했던 모델들은 주변의 이웃 노드들을 종합해서 노드를 임베딩하는 방법들이었다. 오늘은 나무를 넘어 숲을 봐보자. 노드말고 그래프를 임베딩해보자. 딥러닝을 이용한 그래프 임베딩 기법 중 아마 가장 유명한(?) graph2vec(MLG 2017)를 리뷰한다.

그래프2벡의 목적은 기존의 그래프 커널들과 크게 다르지 않다. 유사한 그래프는 가깝게, 아주 다른 그래프는 멀게. Graph similarity evaluation Task를 딥러닝의 관점에서, 익숙한 word2vec의 컨셉으로 풀어본 논문이다. 그래프 커널과 관련된 논문을 읽는 것이 항상 버거운 이유는 알아야 하는 사전 지식이 너무 많고 무겁기 때문이다. 참조되어있는 논문들이 아주 무시무시하지만 Intro는 그냥 짧게 요약하고 넘어가버리자.

• Graph Kernels and handcrafted features
  • 전통적으로 두 그래프 G와 G’의 Isomorphism을 검정하는 알고리즘들
  • handcrafted - 도메인 knowledge에 의존하는 한계를 지녔다

• Learning substructure embeddings
  • GCN, GAT와 같이 Neigbor 구조를 Aggregate하여 노드를 임베딩하는 기법들
  • Entire Graph embedding이 불가능한 구조이기 때문에 Graph Classification에 적용할 수 없다

• Learning task-specific graph embeddings
  • Labeled Data가 아주 많은 supervised setting에서만 좋은 성능을 발휘한다

• 킹왕짱 graph2vec가 가지고 있는 특장점들
  • Unsupervised representation learning
  • Task-agnostic embeddings
  • Data-driven embeddings
  • Captures structural equivalence

• Contribution of graph2vec

  • Propose an unsupervised representation learning technique to learn

    distributed representation of arbitrary sized graphs

  • Demonstrate graph2vec could significantly outperform substructure representation

    learning algorithms and highly competitive to SOTA kernels on graph classification

  • Make an efficient implementaion of graph2vec at Github/graph2vec

PROBLEM STATEMENT

graph2vec이 해결하고자 하는 메인의 퀘스트는 Graph Classification이다. 한 도메인에 여러개의 그래프가 존재할 때, 각 그래프가 어떤 라벨을 가지고 있는 맞추는 문제이다. 앞으로 그래프는 G = (N, E, λ) 이렇게 표현한다. 여기서 N은 노드를, E는 엣지를, λ는 노드의 라벨이라고 정의한다. 라벨이 없는 경우는 그냥 (N, E)로 생각하면 된다. 물론 엣지에도 라벨이 있을 수 있는데, 그런 경우에는 G = (N, E, λ, η) 이렇게 표현해주자.

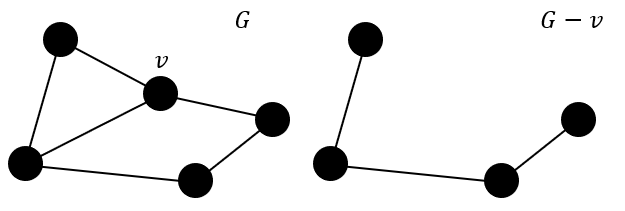
그래프에는 서브 그래프 sg가 존재할 수 있는데, µ : N(sg) → N such that (n1, n2) ∈ Esg iff (µ(n1), µ(n2)) ∈ E가 존재하면 sg가 그래프 G의 서브그래프라고 한다. 어렵게 생각할 것 없이, 작은 그래프의 구조가 큰 그래프의 어딘가에 딱 들어맞게 존재한다면, 작은 그래프가 큰 그래프의 서브그래프라고 보면 된다. 서브그래프를 찾는 전략은 조금 무식하다. 기준이 되는 degree d의 rooted sub-graph를 미리 설정해준 뒤, 모든 노드에서 d-degree에 가능한 모든 경로를 나열한 뒤, 루프를 돌며 해당 노드가 서브그래프의 기준 노드가 될 수 있는지 검정한다.

Background

Skipgram Loss

앞서 서문에서 graph2vec이 word2vec의 컨셉을 계승한다는 말을 했다. word2vec 예기를 하려면 무엇보다도 skipgram-loss를 이해하고 넘어갈 필요가 있다. 우선 skipgramm loss가 목표하는 컨셉적인 목표를 읽어보자. the words appearing in similar contexts tend to have similar meanings and hence should have similar vector representations. 구체적으로 봐보자. 단어를 임베딩할건데, 근처에서 서로 자주 나오는 단어끼리 비슷한 벡터로 임베딩이 될 것이다. 임베딩 세계에서 비슷하다는 소리는 내적했을 때 값을 최대화하겠다는 것을 의미한다. 수식으로 봐보자.

얼마전에 numpy의 결과물이 납득가지 않아서 깃헙에 이슈업을 해봤는데, 짧은 문장 한 두 개를 쓰면서도 구글 번역기를 돌려봐야 될 정도로 영어가 밉고 어렵다. 그럼에도 불구하고 논문을 읽어볼때는, 특히 수식의 근처에서는 꾸역 꾸역 한 문장씩 읽어가며 넘어갈 필요가 있다.

기본적으로 word2vec이 NLP Task이기 때문에 주어진 데이터는 라벨링 된 순서가 있는 단어들의 집합이다. 최대화하고자 목적하는 식은, 단어들간의 조건부 확률이 실제 데이터셋의 빈도와 동일해지기를 바라는 것이다. 단어의 등장이 독립적이라는 가정하에 조건부 확률을 곱셈으로 치환하는 것이 가능해진다. 그럼 결국 최대화하고자 목적하는 확률식을 (타겟 단어 임베딩 · 조건 단어 임베딩) 나누기 sum(타겟 단어 임베딩 · 모든 단어 임베딩) 으로 표현할 수 있게 된다. 바로 이어서 구체적으로 이 확률식을 어떻게 학습하는가에 대한 전략을 살펴보자.

Skipgram Model

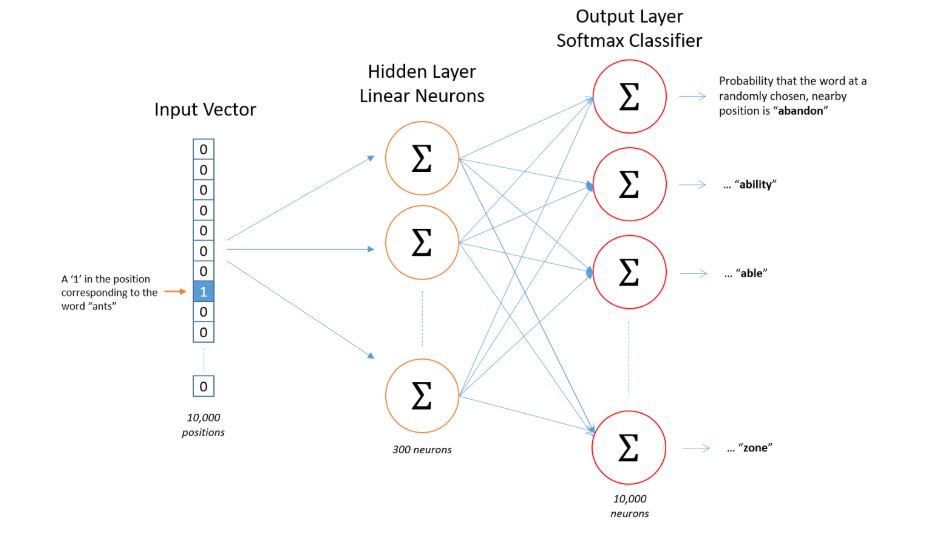
아무 기교를 부리지 않은 본연의 skipgram model은 위의 이미지와 같이 생겼다. 타겟이 되는 단어를 One-hot Encoding하여 인풋으로 모델에 집어넣은 후, 다른 단어들에 대한 확률값을 아웃풋으로 내놓도록 네트워크를 구축한다. 아주 단순한 예를 들어 I LOVE YOU 라는 문장이 있다고 생각해보자. 그렇다면 I를 인풋으로 넣는다는 것은 원 핫 인코딩한 [1,0,0] 이 모델의 인풋으로 들어간다는 것이고, 가까이 있는 LOVE라는 단어에 높은 확률이 나오는 [0.2, 0.6, 0.2] 정도의 아웃풋이 나오는 것이 이상적이다. 모델의 학습 전략을 정리하자면.

1. 모든 문장에 대해 연속된 단어들이 같이 들어가 있는 바구니를 만든다. ## (I,LOVE) , (LOVE,YOU)
2. 원 핫 인코딩한 인풋이 모델을 통과한 후, 합쳐서 합이 1인 확률값을 내뱉는 네트워크를 설계한다.
3. 인풋과 같은 바구니에 들어가 있는 단어들이 높은 확률값을 가지도록 모델을 업데이트한다.

여기에다가 이제 모델의 학습의 전략을 용이하게 만드는 여러가지 기교들이 들어갈 수 있다. 바구니의 사이즈를 2보다 더 크게 설정할 수도 있고, Negative Sampling이라는 전략을 통해 적은 양의 단어들만 학습에 참조할 수도 있다. 더 깊은 내용은 사실 graph2vec을 이해하기 위해서 꼭 필요하지는 않으니 일단 넘어가자.

Doc2vec

아주 참신한 아이디어다. doc2vec 어떤 문단 d를 어떻게 임베딩할 것인가에 대한 전략이다. 각 문단 d에는 어떤 단어w들의 수열 c(d)로 표현할 수 있다. 우리가 Skip gram model을 통해 목적하는 것은 특정 문단의 임베딩이 그 문단에 등장하는 단어들의 임베딩과 비슷해지는 것이다. 분모는 모든 문단들의 단어들이 속해있고, 분자에는 해당 문단의 단어들만 포함되니, 유사한 단어들이 많이 포함된 문단끼리는 비슷한 임베딩을 갖게 될 것을 기대할 수 있다.

LEARNING GRAPH REPRESENTATION

Intuition

그래프2벡은 Doc2vec과 완벽히 동일한 컨셉을 통해 이해할 수 있다. 전체 그래프를 하나의 문단으로, 작은 서브 그래프를 하나의 단어로 대입해보자. 여기서 우리는 어째서 그래프를 이루는 가장 작은 단위가 노드나 엣지가 아니라 서브 그래프여만 하는지에 대한 납득이 필요하다. 논문에서는 두 가지 근거를 제시하는데,

1. Higher Order Structure
   1. 노드 단위로 샘플링을 진행한다고 생각했을 때, 각 샘플은 그래프의 구조적인 정보를 담고 있지 못한다. 그에 반해 서브 그래프 단위의 샘플링은 이웃 노드간의 고오급 정보를 담고 있다.
2. Non Linear Substructure
   1. 가공되지 않은 edge나 path 단위로 구조를 모델링하는 것은 일차원의 linear structure 밖에 정보를 흡수할 수 없다. 기존의 그래프 커널 기법들에서도 WL - Kernel과 같이 non - linear structure를 모델링하는 방법이 random walk kernel에 비해 우수한 성능을 보여줬다.

직관적으로, 결국 우리가 그래프2벡을 수행한다는 것은 고차원의 그래프 데이터를 저차원의 벡터로 임베딩한다는 말인데, 기대하는 바는 고차원에서의 유사함이 저차원의 벡터에서도 유지되기를 바라는 것이다.

Algorithm Overview

doc2vec와 알고리즘 역시 유사하다. skipgram modeling을 위해 여러 문단에서 말뭉치를 먼저 획득하는 것과 마찬가지로, 여러 그래프를 인풋으로 집어 넣어 여러 그래프의 모든 노드들이 가지고 있는 rooted subgraph set을 얻는다. 그리고 얻어진 서브 그래프 데이터 셋을 기준으로 doc2vec과 같은 skipgram modeling을 수행한다. 여기서 한 가지 알아야하는 사전 지식은 서브 그래프를 어떻게 얻을 것인가인데, 논문에서는 WL relabeling strategy를 통해 작업을 수행한다.

사실 WL - Kernel에 대한 리뷰를 하다 말았는데… WL - Kernel paper review 컨셉 정도는 이해할 수 있다.

Input 부터 천천히 봐보자. 우선 D라고 sub graph의 degree를 미리 정의해준다. WL relabeling을 몇 번 수행할지, 몇 hob 까지의 이웃 정보를 취합할지 정의한다. δ는 그래프가 임베딩 된 벡터의 디멘션. e는 skipgramm modeling을 위한 업데이트를 몇 번 해줄지에 대한 hyperparameter이다.

Output은 전체 그래프 셋이 임베딩 되어 G x δ 크기의 매트릭스가 될 것이다.

Algorithm

1. 우선 모든 그래프를 δ 크기로 랜덤하게 임베딩 해준다.
2. 모든 그래프를 학습에 사용하는 것이 아니라 업데이트 될 때마다 기준이 될 그래프 샘플이 계속 바뀐다.
3. 각 G(i) 그래프의 모든 n 노드에 대해 rooted sub graph를 추출하고 skipgram modeling을 수행한다.

WL - Kernel을 통해 rooted subgraph를 추출하는 알고리즘이 따로 서술되어있다.

슈도 코드를 봐도 잘 이해가 가지 않아 깃헙의 코드를 가져와봤다. (알고리즘의 이해에 필요없는 부분들은 삭제했습니다) 아주 길고 복잡한데, 함수 하나 하나를 보기 이전에 메인이 되는 wlk_relabel_and_dump_memory_version 모듈을 살펴보자.

def wlk_relabel_and_dump_memory_version(fnames,max_h,node_label_attr_name='Label'):
    global label_to_compressed_label_map

    graphs = [nx.read_gexf(fname) for fname in fnames]
    graphs = [initial_relabel(g,node_label_attr_name) for g in graphs]

    for it in xrange(1, max_h + 1):
        label_to_compressed_label_map = {}
        graphs = [wl_relabel(g, it) for g in graphs]

    for fname, g in zip(fnames, graphs):
        dump_sg2vec_str(fname, max_h, g)

위에서 부터 쭉 읽어보면,

1. 그래프를 불러오고
2. initial labeling을 수행하고
3. 그래프를 하나씩 돌아가며 wl_relabel을 수행한다.
4. dump_sg2vec_str을 통해 각 노드의 intended subgraph를 얻는다.

def wl_relabel(g, it):
    global label_to_compressed_label_map

    prev_iter = it - 1
    for node in g.nodes():
        prev_iter_node_label = get_int_node_label(g.nodes[node]['relabel'][prev_iter])
        node_label = [prev_iter_node_label]
        neighbors = list(nx.all_neighbors(g, node))
        neighborhood_label = sorted([get_int_node_label(g.nodes[nei]['relabel'][prev_iter]) for nei in neighbors])
        node_neighborhood_label = tuple(node_label + neighborhood_label)
        if not label_to_compressed_label_map.has_key(node_neighborhood_label):
            compressed_label = len(label_to_compressed_label_map) + 1
            label_to_compressed_label_map[node_neighborhood_label] = compressed_label
            g.node[node]['relabel'][it] = str(it) + '+' + str(compressed_label)
        else:
            g.node[node]['relabel'][it] = str(it) + '+' + str(label_to_compressed_label_map[node_neighborhood_label])
    
    nx.write_gexf(g,opfname)

모든 함수 하나하나를 뜯어보지는 말되 wl_relabel의 알고리즘은 순서대로 이해해보자.

• get_int_node_label을 통해 이전 hob에서 취합한 sub graph 구조를 정수로 치환한다.
  • ‘3+1’ (3노드 1노드) -> 31로 치환됨
  • ‘4+3’ (4노드 3노드) -> 43로 치환됨
• 새로운 라벨을 얻는 과정을 기준 노드 뿐 아니라 기준 노드의 이웃들에게도 수행한다.
• 새로 얻어진 라벨들을 다시 ‘+’ 로 묶어준다. (‘31+42’가 새로운 기준 노드의 라벨이 된다)