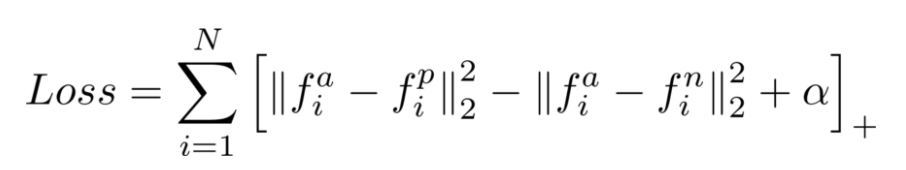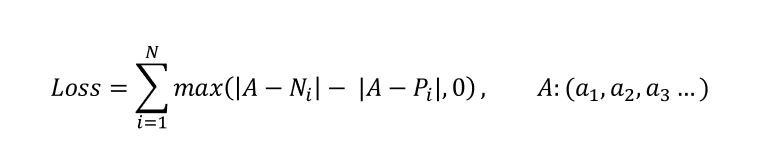달리기를 잘하는 사람을 뽑고 싶습니다. 그런데 잘함이라는 기준은 상대적인 것입니다.
나이에 비하여. 성별에 비하여. 신체 구조에 비하여.
어떤 기준을 갖고 모집단을 분류하고 순서를 매기는가에 따라 잘하는 사람은 다르게 뽑히게 됩니다.
가장 단순하게 생각하면, 가능한 모든 기준을 다 사용하여 집단을 나누고, 그 안에서 정규화한 점수로 순위를 매길 수 있을 것 같습니다. 그러나 데이터가 불균형하면, 특정 소집단에 속하는 사람의 수가 적어 정규화한 값이 쉽게 왜곡될 것입니다.
달리기 실력에 대한 모델링을 해볼까요. 여러가지 기준들을 모두 독립변수로 놓고 적절한 달리기 속도를 구하는 Regression 모델링을 해보겠습니다. 가장 Outlier에 속하는 사람들을 뽑아, 잘하는 사람이라 부를 수 있을 것 같습니다. 그런데 이렇게 모델 에러가 큰 사람들을 뽑고 난 후, 우리가 이것을 진정으로 납득할 수 있을까요? 여러 기준을 각기 다른 가중치로 짬뽕해버리면 이 사람이 누구보다 얼마나 어떻게 잘하는지에 대하여 해석하기가 너무 어려워집니다.
문제를 다시 정의해봅니다. 달리기를 잘하는 사람이 뽑고 싶습니다. 그런데 기준을 어떻게 나누냐에 따라 뽑히는 사람들이 달라집니다. 따라서 우리는 가장 적절한 기준을 먼저 고르고 싶습니다. 가장 적절한 기준이 연령대라고 정해졌다면, 이 사람은 60대치고 달리기를 참 잘하는 사람이다. 이 사람은 20대 중에서도 달리기를 참 잘하는 사람이다. 이렇게 뽑을 수 있을 것 같습니다.
그런데 적절한 기준은 무엇일까요?
우선, 쪼개진 집단간에 평균적인 차이가 나는 것이 자연스러워야 합니다.
만약 쪼개진 다음의 집단간의 차이가 어색하다면, 쪼갤 필요가 없다는 말이 될 수도 있습니다. O형의 사람이 A형의 사람보다 달리기를 잘한다는 말은 자연스럽지 않습니다. 20대의 사람이 60대의 사람보다 달리기를 잘한다는 말은 자연스럽습니다.
더 나아가, 집단간에 겹치는 범위가 없을수록 좋습니다.
만약 몸무게를 기준으로 사람들을 나누어 달리기를 계산해봤을 때, 평균적으로는 가벼운 사람과 무거운 사람간에 차이가 유의미할 수 있습니다. 그러나 분포적으로 봤을 때는 두 집단이 많이 겹쳐져 보일 것 같습니다. 그렇다면 집단내에서 정규화한 점수를 통해 전체를 상대적으로 비교하는 방식이 크게 의미가 없을 수 있습니다. 따라서 집단간에 겹치는 범위가 없는 것이 좋은데요, 집단간에 평균적인 차이가 있으면서 겹치지 않으려면 집단 내에서는 최대한 서로 비슷해야 한다고 말할수도 있을 것 같습니다. 집단내의 분산을 작게 만드는 기준이 좋을 것 같습니다.
일반적으로는 multi factor ANOVA 등을 통해 평균의 차이를 가장 유의미하게 만들면서 가장 독립적인 변수를 찾아 볼 수도 있을 것 같습니다. 그런데 통계는 재미가 없고 어렵습니다. 머신 러닝은 재밌고 직관적이죠. 추천 시스템의 학습에 자주 이용되는 Triplet Loss를 응용하면 저희가 직면한 문제를 해결할 수 있을 것 같습니다.
Triplet Loss
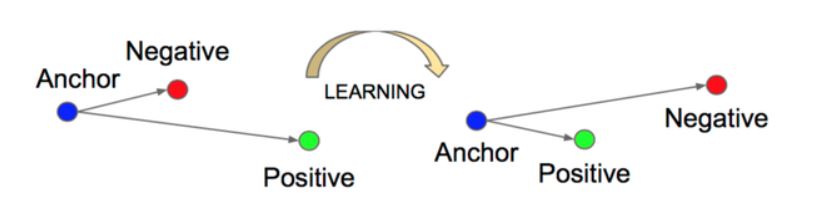
최대한 간단하게 설명해보겠습니다. 추천 시스템의 학습 목표는 의자를 검색한 사람한테 쇼파를 추천하는 것입니다. 의자를 검색한 사람한테 홍삼을 추천하고 싶지 않습니다. 따라서 학습은 시스템이 의자와 쇼파를 가깝다고 인지하게 만들어야 합니다. 의자와 홍삼은 멀다고 학습시켜야합니다.
위의 이미지를 봐보겠습니다. Anchor는 의자입니다. Positive는 쇼파입니다. Negative는 홍삼입니다. 학습은 Loss 최소화하는 것이겠죠? 여기서의 Loss는 의자와 쇼파의 거리가 멀고, 의자와 홍삼이 가까울수록 커지게 됩니다.
이걸 식으로 보면 아래와 같습니다.
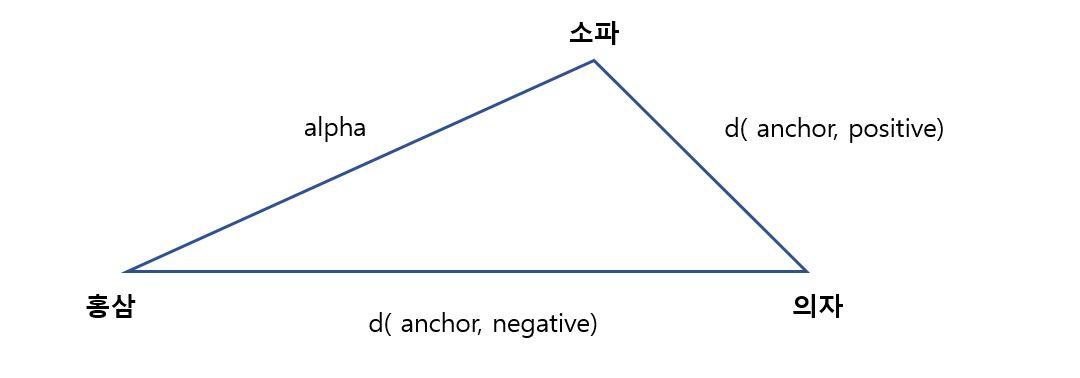
식의 뒤에 붙은 알파 값은 홍삼과 쇼파의 거리를 의미합니다. 이차원적으로 아래와 같이 그릴 수 있을 것 같습니다.
이차원적으로 보면 단순히 거리뿐만 아니라 둔각을 크게 만드는 방향으로도 적용할 수 있을 것 같습니다. 이렇게 각도와 거리를 우리가 의도한 학습 방향에 맞게 적절하게 조절하다보면 추천 시스템이 학습된다고 합니다.
그런데 추천 시스템은 잘 모르겠고. 우리가 직면한 문제에 이것을 어떻게 접목하는지가 중요한 것이겠죠.
우리의 목표는 집단간의 평균은 크고, 집단내 분산은 작게 만드는 기준을 찾는 것입니다.
적적한 기준으로 모든 사람들을 나누었더니, 그룹간에는 차이가 많이 나고, 그룹내에서는 차이가 적게 납니다.
각 그룹내의 사람들은 전체 평균과는 최대한 멀리 있고, 그룹 평균과는 최대한 가까이 있습니다.
전체 평균을 Negatvie, 그룹 평균을 Positive라고 한다면 각 기준의 로스를 아래와 같이 표현할 수 있습니다.
- 각 기준이 몇 개의 그룹으로 전체 집단을 나누는가에 따라서 N의 개수는 달라질 수 있습니다.
- 가장 작은 로스를 만드는 기준이
군집간에는 멀고 군집내에서는 가깝게잘 나누었다고 해석할 수 있습니다.
달리기를 잘하는 뽑고 싶다는 예시 외에도, 고객을 세분화하고 싶을 때 이런 문제를 자주 마주하게 됩니다.
과금을 많이 한 유저가 누군지 알고 싶을 때
- 즐기는 게임에 따라서 / 연령대에 따라서 / 총 플레이 시간에 따라서
샷발이 좋은 스나이퍼가 누군지 알고 싶을 때
- 맵에 따라서 / 계급에 따라서 / 적 팀의 수준에 따라서
기준을 어떻게 잡고 세분화하는 가에 따라서 추출되는 고객이 달라지게 됩니다. 따라서 우리가 사용하려는 기준이 다른 사용 가능한 것들에 비하여 적절한지에 대하여 검증해보면 좋을 것 같습니다. 우리가 사용하려는 기준이 정말 로 상대적 우위를 비교하기에 적절한 것인지.