다음에 나올 결과를 확률적으로 뱉어내는 random function이 있을 때, Stochastic Process는 해당 function space의 random element로 해석된다. 맞다. 괜히 어려운 말인척 해봤다. 요번 강의에서 Stochastic Process는 단순히 시간에 따라 생성되는 Random Variable의 모음이다. 좀 더 멋지게 표현하고 싶으면 Probability distribution over a space of paths라고도 말할 수 있다고 한다.
Lecture 5. Stochastic Process I
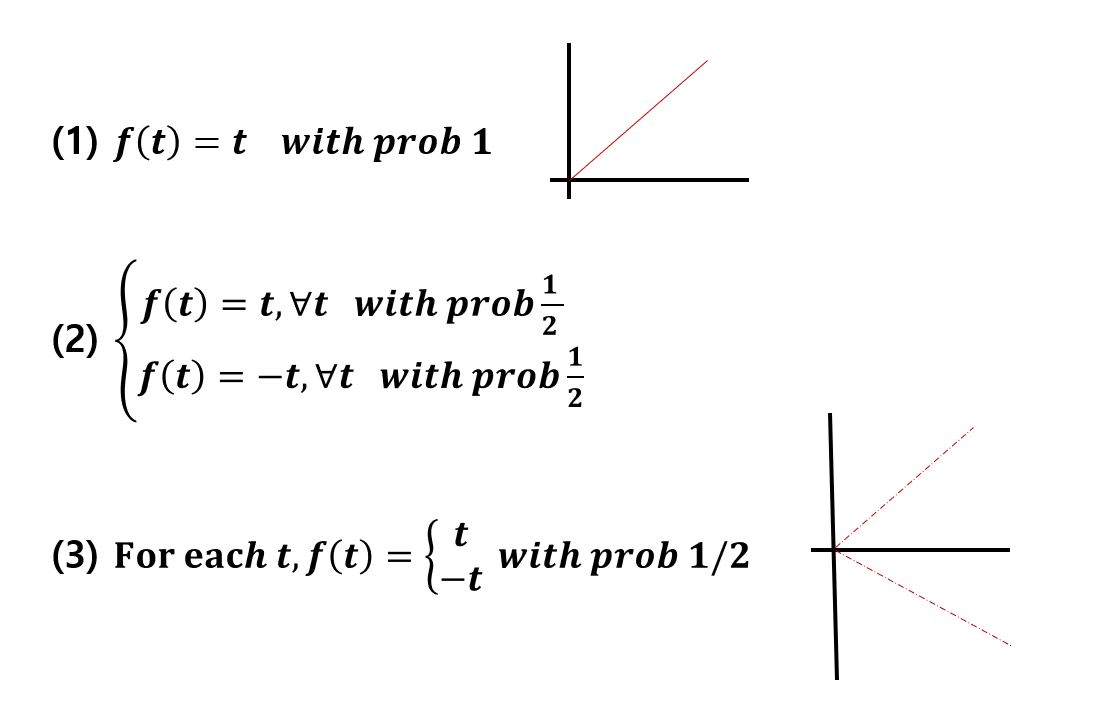
위의 3가지 예제는 모두 어떤 확률에 의해 값이 정해지는 Stochastic Process 이다. 그러나 마지막 하나의 함수는 한 가지 다른점이 있는데, 바로 f(t)의 독립성이다. 위의 두 함수는 한 시점의 f(t) 값을 아는 순간, 나머지 모든 순간의 f(t) 값은 결정되며 종속적이다. 그러나 세 번째 케이스의 경우, 여태까지의 모든 값을 알았다고 한들 다음 t+1 시점의 값은 여전히 확신할 수 없다. 그리고 앞으로의 수업에서는 이런 불확실한 Stochastic Process를 다루는 법에 대한 것이다.
두 개로 나누어 질 Stochastic Process 강의 중, 요번 강의는 discrete time 위에서의 특징들을 알아본다. 그리고 수업 전반적으로 궁금해 할 3가지 특징은 아래와 같다.
- What are the dependencies in the sequences of values?
- What is the long term behavior?
- What are the boundary of events?
Simple Random Walk
오늘 수업에서는 3가지 Stochastic Process를 다루는데 그 중 가장 간단한 형태인 simple random walk를 알아본다. 근처에서 예시를 찾아보면 동전던지기 놀이가 있다. 완벽히 동일한 확률의 두 경우가 존재하며 기대값이 0으로 떨어지는 Random Variable.
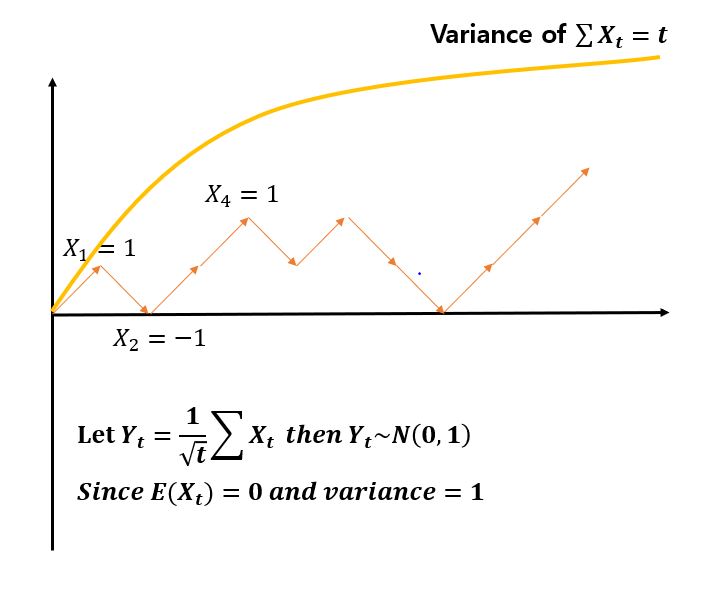
Simple Random Walk는 동전을 던진 횟수 t를 x축으로 놓고, 앞면이면 X(t) = X(t-1) + 1 뒷면이면 X(t) = X(t-1) -1하며 한 칸 씩 위나 아래로 움직인다. 기대값이 0이고 분산이 1인 Simple Random Walk를 아주 큰 t까지 확장해서 생각해보자. 지난 수업에서 다루었던 Central Limit Theorem의 정의를 생각해보면 아래와 같이 랜덤 워크를 통해 얻어진 Y(t)가 정규분포의 형태를 띔을 알 수 있고, 우리는 t시점에 Y(t)의 값이 정규분포에서 크게 벗어나지 않는 어딘가에 있을 것이라 기대할 수 있다.
Property
- E(X_t) = 0
- Independent Increment
- X_t - X_t-1 값은 t의 값에 상관없이 독립적이다.
- t시점에서 위로 갈지 아래로 갈지는 과거의 값을 통해 유추할 수 없다.
- Stationary
- 어떻게 구간을 잘라도 구간의 첫 시점의 값을 빼고난 후의 분포는 X_t가 된다.
Example
t = 0에서부터 X_t가 위아래로 한 칸 씩 움직일 것인데,
X_t가 $100 혹은 -$50가 되면 동전던지기 게임을 그만둘 것이다.
$100을 먼저 터치하여 게임이 끝나는 확률은 어떻게 구할까?
풀이
![]()
Markov Chain
Stochasitic processes whose effect of the past
on the future summarized only by the current state
= Simple Random Walk is one of Markov Chain
사실상 마르코브 체인은 Transition Probability Matrix를 구하면 모든게 끝나는 느낌인데, 이 매트릭스가 뭐냐면 가능한 여러 상태간의 확률들이 정리되어 있는 표와 같다고 보면된다. 우리는 이런 느낌의 확률 문제를 많이 경험해왔었는데, 예를 하나 들어보자.
(Example) Machine Broken or Working at a gived day
이렇게 오늘의 상태가 작동 혹은 고장일 때, 내일의 상태가 작동일 지 고장일 지 확률을 알고 있을 때, 이렇게 표 형태의 확률 정보들을 Transition Probability Matrix 라고 이름 부르는 매트릭스 형태로 아래와 같이 표현하면 된다.
위의 Transition Matrix는 오늘 -> 내일의 하루치 상태 변화에 대한 정보가 담긴 행렬이라고 볼 수 있다. 그렇다면 오늘 -> 내일 모레의 이틀치 상태 변화가 담긴 행렬은 어떻게 생겼을까? 직관적이게도 저 행렬을 제곱함으로서 얻을 수 있다. 마찬가지의 개념으로 만약 오늘 -> 10년 후의 상태에 대한 확률이 얻고 싶으면 행렬을 3650번 제곱하면 된다. 그리고 아래와 같은 사고 흐름을 통해 10년 후의 기계의 상태는 Transition Matrix의 largest eigenvector vector를 추출하는 것과 같은 일이라는 것을 알 수 있다. 즉, Markov Chain의 long term behavior을 나타내는 어떤 벡터 v를 얻을 수 있다.
Martingale
Stochastic process which are fair game
Random Walk is a martingale
Balance of a Roulet player is not a martingale
마팅게일 예제
![]()
Optional Stopping Theorem
[DEF] Stopping TimeGiven a stochastic process {X(1),X(2)…} a non-negative integer random variable τ is called a stopping time if fore all integer k >= 0, τ <= k depends only on X(1),X(2)…X(k)
= the strategy only belongs to present value
Example
- $100 or -$50 달성시에 동전 던지기 게임을 그만한다. <- O (오직 현재의 값을 기준으로 Stop)
- 첫 번째 피크를 달성시에 동전 던지기 게임을 그만한다. <- X (고점이 지난 뒤에 알 수 있으니깐)
[Thm]Suppose X0,X1,X2, … martingale & τ is a stopping time
And futher suppose that there exists a constant T such that τ <= T always (Finite time strategy)
Then E[X(τ)] = X(0)
==»
CorIt applies case ($100 or $-50), E[X(τ)] = 0
E[X(τ)] = p x 100 + (1-p) x -50 = 0 , So, p = 1/3
만약, 어떤 문제가 martingale을 사용해서 모델링 될 수 있다면 이기거나 질 것이라 기대할 수 없다.