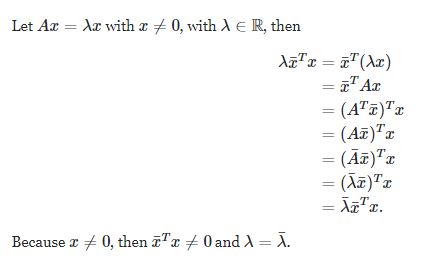Lecture 2. Linear Algebra (18.S096)

전공 과목 중 금융 수학이라는 과목이 있었는데 구체적으로 무엇을 배웠고, 어디에 쓸 수 있는 수학이었는지가 당최 기억이 나지 않는다. 다만 한창 비트코인 열풍의 시기라 수업의 주제가 매우 흥미로웠고 알아두면 쓸모 있을 것 같은 느낌만이 느낌적으로 남아있다. 시간을 되돌려 수업을 진중하게 들어볼 수 있다면 좋겠지만 그럴 수 없으니 MIT OpenCourseWare에서 비슷해 보이는 강의를 찾아보았다.

MIT 18.S096 Topics in Mathematics with Applications in Finance, Fall 2013 Youtube 링크

Lecture 1. Introduction, Financial Terms and Concepts

• KEY FACTS
  • The purpose of the class is to expose the mathematical concepts and techniques used in finance
  • Prerequusutes:
    • 18.01 Single Variable Calculus
    • 18.02 Multivariable Calculus
    • 18.03 Differential Equations
    • 18.05 Introduction to Probability and Statistics
    • 18.06 Linear Algebra

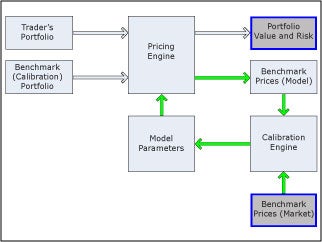
인트로 강의는 크게 두 파트로 나누어져 첫 파트에서는 시장 경제의 역사적 흐름을 소개한다. 과거, 특히 최근의 30년간 수학과 컴퓨터 사이언스가 어떻게 Trading 시장에서 중요한 역할을 하게 되었는지. 뒤의 파트에서는 앞으로의 클래스에서 무엇을 배울지 몇 개의 예시로 보여준다. Monte Carlo pricing / Kalman Filter 등을 사용하여 주가를 예측하는 프로젝트를 진행하려나 보다?

Lecture 2. Linear Algebra

금융 수학을 이해하기 위한 선형 대수학의 핵심적인 개념들을 리뷰한다. 가장 간단한 선형대수 강의를 수강한 학생들을 기준으로 수업을 진행한다.

Matrix

• A collection of Numbers
• 매트릭스에는 어떤 정보가 담길 수 있을까?
  • Row: Company
  • Column: Date
  • 각 셀에는 주가가 들어있는 형태의 Matrix Data를 생성한다.
• 매트릭스 형태의 데이터는 왜 강력할까?
  • Theoretical point of view
  • A: m x n matrix
  • A: R^n –> R^m 차원으로 사영하는 linear transformation의 역할을 수행한다.

Eigenvalue, Eigenvectors

• Happens iff det(A - λ*I) = 0

• det(A - λ*I) is a polynomial of degree n in terms of λ

• Eigenvalue의 기하학적 이해

  • 어떤 벡터 v에 Matrix A의 operation이 가해진 것이, v를 λ만큼 스케일 업 한 것과 같다.

    
    

• Matrix A가 orthonormally diagonalizable한 것의 의미

  • A = UDU_t (U_t: U transpose)

  • U: orthonormal Matrix, D: diagonal Matrix

  • 그러면 U는 A의 Operation이 표현하는 방향이 되고, D는 각 방향의 크기를 나타낸다.

    (Thm 1) All symetric matrices are orthonormally diagonalizable

    (Thm 2) Real Symmetric Matrix have real eigenvalues

    

    ( Proof Thm2 ) 대충 람다의 complex conjugate가 람다와 동일하니 람다가 실수라는 뜻

What about general matrices? Not all matrices are diagonalizable

Want to still understand the matrix A through “simple” operations

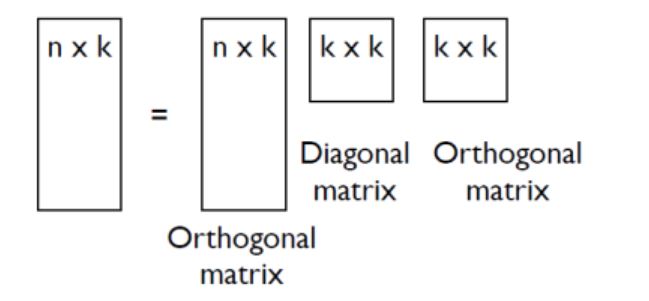
Singular Value Decomposition

(Thm 3) A: m x n matrix, There always exists orthonormal matrics U and V

such that A = U * ( ∑ ) * V_t for some diagonal matrix ∑ (U: m x m, ∑: m x n, V: n x n)

Theorem3은 U와 V가 각각 (A * A_t) / (A_t * A) 의 eigenvoctor를 컬럼으로 갖는 orthonormal matrix가 됨을 보이는 방식으로 증명할 수 있다. 구체적인 것은 Gundersen님의 블로그를 쭉 읽다보면 알 수 있다.

예를 들어, 어떤 행렬 A가 3 x 2의 형태로 이루어졌다고 생각해보자. 먼저 det(A_t * A - λ) = 0이 되게 만드는 λ를 구하여 eigenvalue를 구해준 다음 3개의 eigenvector를 컬럼으로 갖는 V를 찾을 수 있다. 이후 U는 λ와 V를 통해 유도하여 2 X 2 형태의 매트릭스를 얻을 수 있다. AA_t에서는 0 보다 큰 eigenvalue가 2개만 얻어지기 때문에 V의 3번째 컬럼은 irrelevant 하다. 다시 말하자면 eigenvalue 0에 대응하는 eigenvector는 쓸모가 없다. 따라서 아래와 같은 simplified form으로 Singular Vlue Decomposition을 수행해도 결과는 달라지지 않는다.

• 회사와 주식 가격들이 시계열로 기록되 있는 Matrix에서 Eigenvector는 무엇을 의미할까?

  • m개 company의 n개 dates에 대한 stock prices가 기록된 행렬 A가 존재할 때,

    (A * A_t)는 m x m의 행렬이 되며,

    해당 행렬의 eigenvector를 통해 m개 컴퍼니의 correlation을 표현할 수 있다 (?)

(Thm 4 Perron–Frobenius theorem)

A: n x n symmetric matrix with positive entries, Then

1. Some real Eigenvalue λ0 such that abs(λ) < λ0 for all other λ exist
2. Some eigenvector with all positive entries corresponding to λ0
3. λ0 is an eigenvalue of multiplicity 1

SVD의 대상이 되는 주식 가격 행렬을 A * A_t 취한 행렬이 위의 이론들을 따르기 때문에 나중에 마르코프 체인을 이론적으로 설명할 때 여러 이득을 취할 수 있다고 한다. 뒤에를 마저 들어야 뭔소린지 알 것 같다.