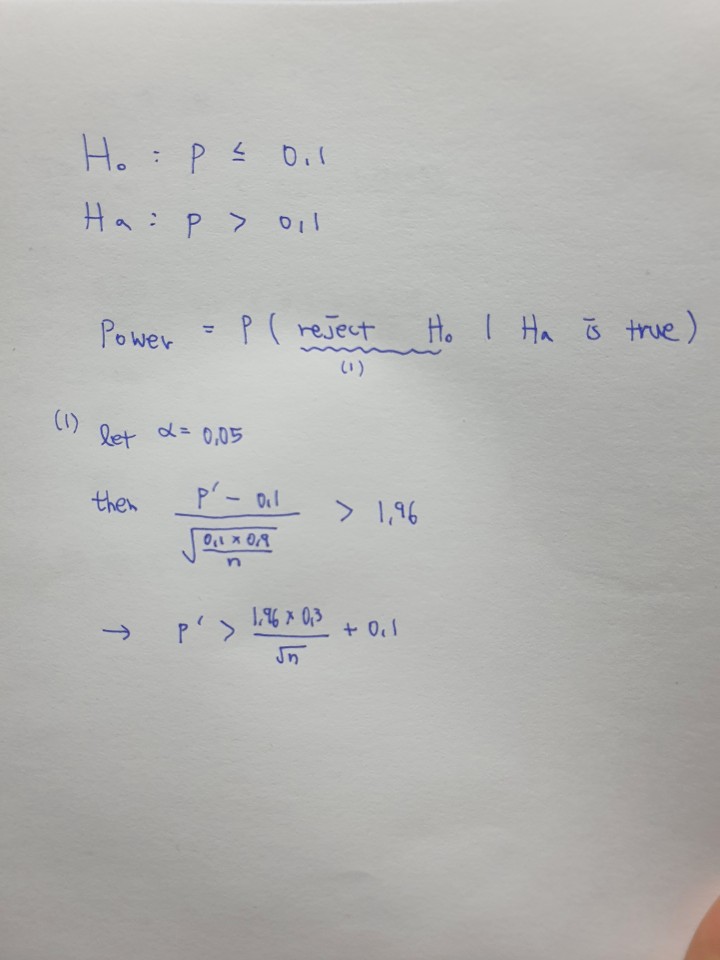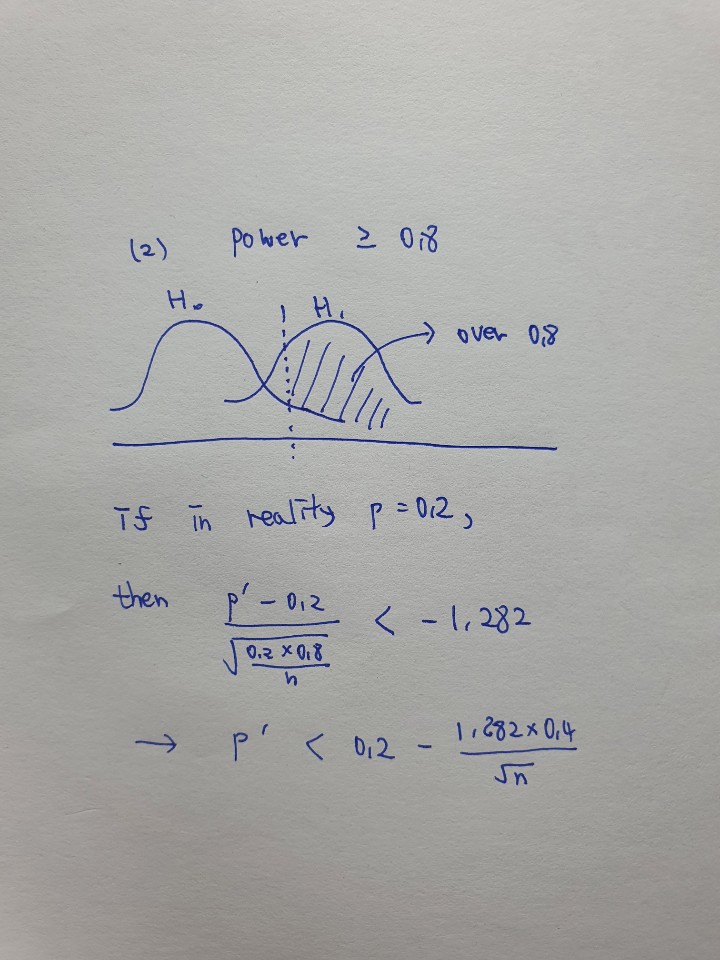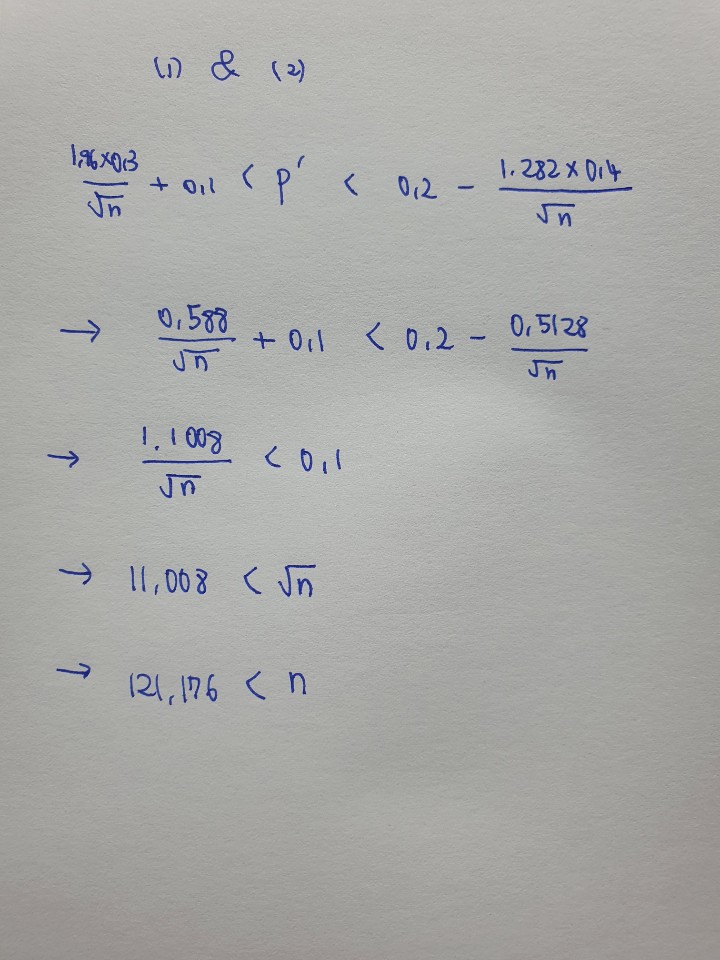중심극한정리는 통계를 쉬워 보이게 도와줍니다. 적당히 큰 N에 대해서 분포들의 평균은 언제나 정규분포를 따른다. 그러니깐 p-value든 z socre든, 대충 정규분포를 가정하여 계산하고 검정에 사용하라 말해줍니다. 그런데 정말 그럴까요? 미신처럼 내려오는 마법의 샘플 숫자 30개.. 믿어도 될까요?
참조
- Statistical Power Analysis for the Behavioral Sciences(1988)
- (Youtube) Power Analysis, Clearly Explained!!!)
검정력 분석(Power Analysis)은 검정력(Power)이 몇인지 구하는 분석입니다.
검정력은 귀무가설이 틀렸을 때, 귀무 가설이 틀렸다고 할 확률입니다.
동전 던지기를 해보겠습니다.
우리의 귀무 가설은 앞면과 뒷면이 나올 비율이 모두 50%라는 것입니다.
그런데 동전의 앞면이 나올 비율이 사실은 60% 였다고 가정해봅시다.
그러면 실제로 귀무가설이 지금 틀렸다는 것이겠죠?
이제 실제로 실험을 한 후, 동전의 앞뒤면의 비율이 다르다고 말 할 확률이 바로 검정력입니다.
검정력 분석은 대게 두 경우에 사용됩니다.
- A priori: compute N, given alplah, power, effect size
- Post-hoc: compute power, given alpha, N, effect size
A priori power-analysis는 실험을 기획하는 단계에서 실험에 적절한 N이 몇인지 정하는 분석입니다. Post-hoc power-analysis는 실험을 수행하고 난 뒤, 실험의 검정력이 타당한가를 확인하는 분석입니다. 그런데 Post-hoc은 정말 통계통계한 소수의 영역인 것 같고, 대체로 우리에게 필요한 것은 A priori power-analysis 입니다.
A priori는 유의 수준, 검정력, Effect Size가 주어졌을 때, 적정 샘플의 크기 N을 구하는 분석입니다.
Effect Size는 집단간의 실제적인 차이를 의미합니다. Effect Size를 구하는 방법이 하나는 아닙니다.
예를 들어, 두 집단에서 남녀의 비율이 하나는 0.6, 하나는 0.5였다고 생각해봅시다.
Effect Size는 실제적인 차이를 의미합니다. 두 비율을 뺀 0.6 - 0.5 = 0.1이 Effect Size가 될 수 있습니다.
혹은 두 비율값의 Ratio인 0.6 / 0.5 = 1.2가 Effect Size가 될 수도 있습니다.
Cohen h formula라는 것을 사용하여 구할수도 있습니다.
- Cohen’h
- p1, p2간의 Effect Size h
- h = abs( arcsin(root(p1)) - arcsin(root(p2)))
우리의 목표인 적절한 Sample Size N 을 구하는 문제를 하나 풀어보겠습니다.
상자안에 파란 구슬과 빨간 구슬들이 들어가있다.
파란 구슬을 꺼내는 비율이 모든 시도에서 0.1보다 작다고 기대하고 있다.
그런데 알고보니 실제로는 파란 구슬을 꺼낼 비율이 0.2였다.
이런 경우에, 0.01 유의 수준내에서, 파란 구슬을 꺼내는 비율이 0.1보다 크다고
할 확률이 0.8 이상이었으면 좋겠다.
위의 조건들을 모두 만족시킬 최소의 시도 횟수 N은 몇일까?
위 문제의 조건들이 갖는 의미
- 우리의 기대는 0.1 그러나 실제는 0.2
- Effect Size를 확률간의 차이로 놓았을 때, 위 문제의 Effect Size는 0.1이다.
- 귀무 가설 기각의 기준이 되는 유의수준 alpha는 0.01이다.
- 실제 비율이 0.2일 때, 귀무 가설을 기각할 확률이 0.8 이상
- type 2에러를 발생하지 않을 확률인 power는 0.8이다.
(조건 1) Power는 실제로 귀무 가설이 틀렸을 때, 틀렸다고 말 할 확률입니다.
→ Power는 대립 가설이 맞았을 때, 귀무 가설을 기각 할 확률입니다.
→ Power = P(reject 귀무 가설 when 대립 가설 is true)
- 지금 우리의 문제에서 대립가설은 p = 0.2입니다.
우선은 위 이미지와 같이 유의수준 0.01내에서 귀무 가설을 기각시키는 표본 평균의 범위를 구합니다.
귀무 가설을 기각하기 위해서는 z-value가 임계값인 1.96보다 큰 값이어야 합니다.
(조건 2) 우리가 설정한 power는 0.8입니다. type 2 error는 0.2보다 작아야 합니다.
→ P( p < 조건1을 만족시키는 p’ when p = 0.2) = type2 error
→ P( z < (p’-0.2) / sd) = type2 error
type2 error가 0.2보다 작기 때문에 (p’ - 0.2) / sd는 신뢰수준 80%의 z-value인 -1.282보다 작아야 합니다.
조건을 모두 만족하는 N의 최소값보다 큰 수가 실험을 위한 적정 Sample Size라고 볼 수 있습니다.