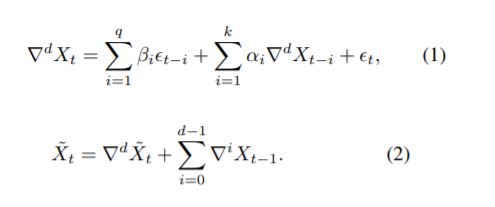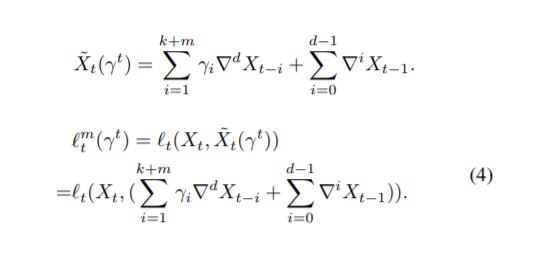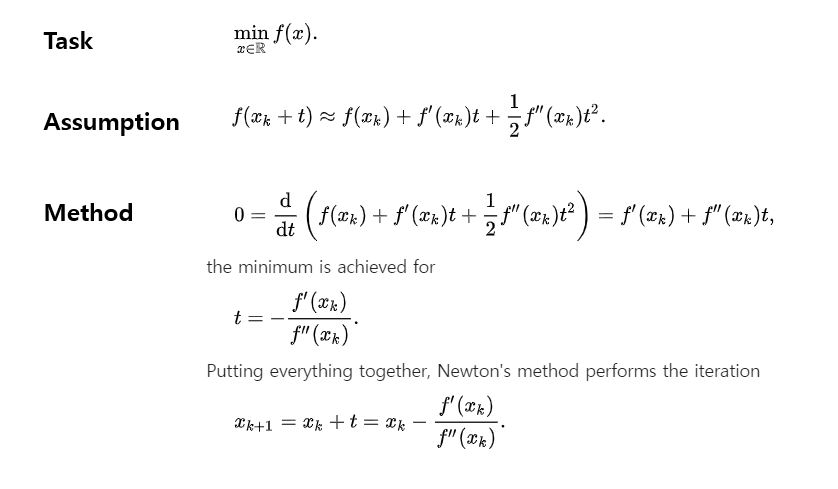Online ARIMA
처음에 제목을 읽었을 때, Online ARIMA? 온라인에서 만들어지는 시계열을 예측하는건가? 싶었다. 물론 그런 단순한 작명은 아니었다고 한다. 설명이 많지는 않지만 위키피디아에 따르면 online model이란,
An online model is a mathematical model which tracks and mirrors a plant or process in real-time, and which is implemented with some form of automatic adaptivity to compensate for model degradation over time
수학적인 모델링을 통해 실시간으로 최적화되는 모델을 통칭하는 용어라고 보면 되나 보다. 그럼 online이 아닌 모델은 무엇인가? 멀리 갈 것 없이 기존의 ARIMA 모델을 보면 된다. 논문에 따르면 ARIMA는 However, its parameters are estimated in a batch manner. 학습된 상태에서 새로운 데이터에 대한 국소적인 업데이트가 가능한 구조가 아니다. parameter를 도출하는 기존의 least squares / maximum likelihood 베이스의 방법들은 모든 데이터에 대한 접근을 선행해야 하기 때문이다. 논문에서 ARIMA 모델링을 어떻게 Online model optimization task로 치환하였는지는 뒤에서 구체적으로 봐보자.
Linear Regression
논문을 살펴보기 전에, 모델 혹은 데이터가 Linear 하다는 것의 의미를 알고 넘어가자. ARMA는 모델이 Linear하다는 것을 가정하고 있어 현실에 적용하기에 무리가 있었고, Integrated term을 추가한 ARIMA 모델이 등장하게 되었다. Integrated term을 통해 모델을 Linear하게 만드는 것은 무슨 말일까.
Integrated (I) represents the differencing of raw observations to allow for the time series to become stationary, i.e., data values are replaced by the difference between the data values and the previous values
그보다 우선하여 Linear regression이란 무엇일까? 사실 이름만 보면 linear regression은 직선? non linear regression은 곡선인가? 오해할 수 있다. 오해를 풀기 위해 linear regression과 non linear regression의 정의를 살펴보면,
In statistics, a regression model is linear when all terms in the model are one of the following:
- The constant
- A parameter multiplied by an independent variable
즉, 모델의 linearlity는 Output의 형태가 아니라 parameter의 linearlity에서 비롯한다.
예를 들어, 위의 Y를 실제로 그려보면 곡선이 나오지만 이것은 Linear Regression이다. 모든 파라미터 베타들이 상수거나 혹은 independent variable에 곱해져있기 때문이다. (1, X, X^2는 서로 linearly independent하다) 정리하자면 주어진 Y를 표현할 때, 모든 파라미터들을 independent variable 단위로 쪼개서 equation을 생성할 수 있다면 우리는 linear modeling을 수행한 것이다.
ARMA 모델로 돌아와보자. 실측치와 predict error를 몇 개까지 볼 것인지를 조정하며 여러 형태의 ARMA 모델이 등장할 수 있다. 예를 들어, ARMA(2,1)을 살펴보면 파라미터 파이1과 파이2가 각각 y(t-1)과 y(t-2)에 곱해져 있다는 것을 볼 수 있다. 근데 만약 y가 non -stationary 하다면 어떻게 될까. 두 변수간의 correlation coefficient가 0이 아니라면 그 둘은 더 이상 independent하다고 볼 수 없고, ARMA 모델은 더 이상 linear modeling이 아니다.
그렇다면 integrated term을 통한 differencing of raw observations은 어떻게 데이터를 stationary하게 만들까? 우선 stationary의 정의를 살펴보면,
In mathematics and statistics, a stationary process is a stochastic process whose unconditional joint probability distribution does not change when shifted in time
즉, y의 평균과 분산 그리고 correlation이 x가 변함에 따라 변하지 않아야 한다. y = x + b라는 식을 생각해보자. 해당 직선은 x가 증가함에 따라 분산은 변하지 않지만 y의 평균이 지속해서 증가한다. 따라서 y는 stationary하지 않다. 근데 만약 x를 x’으로 바꾸고 (x’(t) = x(t) - x(t-1)) , y = x’ + b를 그려보면 어떨까. 해당 식의 y는 항상 평균이 b이고 분산이 0인 stationary한 상태가 된다. 이렇게 데이터를 한 번 혹은 그 이상으로 차분하여 데이터를 stationary한 상태로 바꾸어 ARMA 모델의 linear modeling assumption을 가능하게 하는 것이 ARIMA 모델이라고 볼 수 있다.
Contribution of paper
다시 논문의 리뷰로 돌아와 기여한 바를 살펴본다.
- Propose a novel online learning method to estimate the parameters of ARIMA models by reformulating it into a full information online optimization task
- Theoretically, we give the regret bounds which show that the solutions produced by our method asymptotically approaches the best ARIMA model in hindsight
- Experimental result empirically validates that online ARIMA algorithms considerably outperform the existing online ARMA algorithms
Online ARIMA Algorithm
ARIMA가 어떻게 predict에 사용되는지 수식적으로 확인해보자. 노테이션이 조금 헷갈릴 수 있지만 (1) 식의 differential(d) 처럼 표현되어 있는 것은 주어진 sequence X가 d 번 차분되었다는 것이다. X의 형태에 따라 몇 번의 차분으로 stationary한 상태가 될 수 있는지 달라지기 때문에 d는 학습되어야 하는 parameter 중 하나이다. 주기성이 없다면, ARIMA에 필요한 parameter는 3가지다.
ARIMA(k,d,q)
- k: 차분된 데이터를 과거 몇 개까지 활용할지
- d: 데이터를 stationary하게 만들기 위한 차분의 횟수
- q: 이전의 예측값과 실측값의 오차를 과거 몇 개까지 활용할지
(2)번 식은 차분된 데이터를 통해 모델링 된 ARIMA를 실제로 predict에 활용한 수식이다. 차분된 상황에서의 시점 t에서의 값을 (1)식을 통해 얻고, stationary되기 위해 차분된 값을 다시 역으로 더해 실제값에 대한 예측을 수행한다.
Online ARIMA 알고리즘의 목적함수는 일반화하여 위와 같이 표현할 수 있다. 새로운 T개의 data에 대한 실측값과 예측값의 차이를 최소화하도록 ARIMA의 parameter가 업데이트 될 것이다. 그런데, online 모델링 process에서 parameter q에 대해서는 학습할 수 없다. 과거의 실제값에 대한 정보는 주어지지만 예측값에 대해서는 알 수 없기 때문에 이전 시점의 오차를 모델링에 활용할 수 없기 때문이다. (MA process는 white noise를 사용하는 모델링이기 때문에 둘 이상의 미래에 대한 예측이 불가능하다) 따라서 ARIMA(k, d, q)를 근사하는 modified ARIMA(k+m, d, 0)가 대신 사용될 것이다.
If the ARMA process is causal and invertible,
it can be written either as AR (MA) process of infinite order
이제 남은 과제는 기존 모델을 잘 근사할 수 있는 m을 찾는 일과, m+k개의 AR parameter를 어떻게 최적화 할 것인가이다. convex - optimization solver는 여러 알고리즘이 존재하지만, 논문에서 제시하는 두 가지 방법은 newton-step & gradient descent 이다. 두 알고리즘을 통해 어떻게 모델의 parameter를 적합하고, 각 알고리즘의 loss upper bound는 어떻게 이론적으로 추정되는지 살펴본다.
ARIMA Online Newton - Step (ARIMA-ONS)
수치 해석 시간에 분명 봤던 것 같은 기괴한 기호들로 이루어진 알고리즘 식을 이해하려면 우선 newton’s method in optimization이 무엇인지 부터 알고와야 한다. 위키피디아를 읽어보자.
Newton’s Method
Newton’s method는 iterative한 과정을 통해 위의 Task를 수행하는 것을 목적한다. 즉 처음에 initialize한 x(0)에서 출발하여 각 반복에서 x를 t만큼 조정해주면서 지역해를 찾는 과정이다. 여기서 들어가는 Assumption은 tayler expansion에서 2차 미분까지의 값 만큼만 사용하여 추정한다는 것이다. 프사이를 막 엄청써서 충분히 유사하다고 수업 때 증명했던 것 같다. 기억 안 난다. 여기서 지역해를 찾고자 목적하는 함수 f의 2차 미분이 양수일 때, f(x + t)의 미분값이 0이라면 우리는 지역해에 도달한 것이다. 물론, expansion에서 2차 까지만 사용하여 완벽한 추정이 아니기 때문에, 이렇게 x를 조금씩 옮겨주는 과정을 반복해줘야 한다.
그러나 이것으로는 newton’s method를 적용할 수 없다. 위의 경우는 f가 x 하나만으로 이루어졌다고 가정한 상황이었기 때문에 high dimensional 케이스로 newton’s method를 일반화할 수 있어야 한다. 아주 직관적으로 설명해주는 글이 여기에 있으니 읽어보자.
우선 알고리즘에서 먼저 눈에 띄는 것은 m을 세팅하는 부분이다. ARMA(a,b) 모델을 AR(a+m) 모델로 근사하기 위해서 적절한 m을 찾아야하는데 알고리즘에 언급된 저 방식은 무엇일까. 놀랍게도 논문의 어디에도 저게 뭔지 설명해주는 부분이 없다. 독자라면 알아야 할 기본 상식 같은 것인가 보다.
TLM: Maximum likelihood estimation for heteroscedastic t regression
이것이 무엇이냐면.. 여기를 봐보자.
heteroscedastic은 시계열에서 일반적으로 changing or unequal variance across the series를 뜻하는데
요약하자면 error가 independent value의 값에 독립적인지 확인하는 방식이다.
ARMA process를 통해 얻어진 노이즈와 같은 분포를 갖도록 AR 모델을 수정하는 것(?)이다.
라고 추측한다.. 아마 [여기](file:///C:/Users/littl/Downloads/12135-55701-1-PB%20(2).pdf 논문의 내용으로 설명되는 것이라고 추측한다..
사실 그 뒤의 업데이트 부분은 매우 일반적이다. 로스는 error의 분산을 통해 계산하고, newton’s method의 방식으로 얻어진 t를 미리 설정해놓은 learning-rate만큼 곱하여 기존의 parameter를 업데이트 해준다. 이런 작업은 예측에 사용한 모든 T개 시점에 대해 병렬적으로 수행되는 것이 아니라 iterative하게 이루어진다.