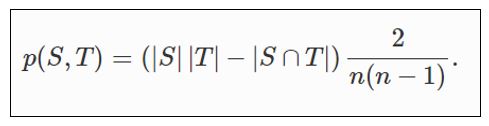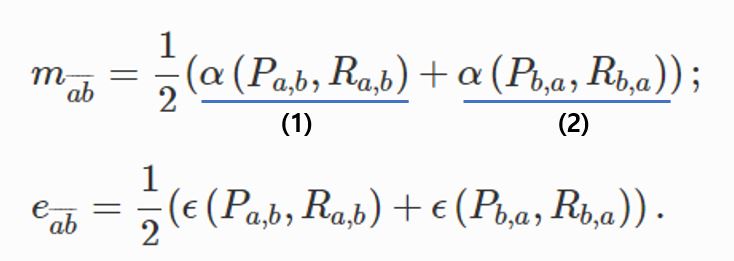어떤 데이터와 문제는 그래프로 표현하고 그래프로 해결해야 효과적인 경우가 있다. Outlier Edge Detection은 말그대로 이상한 연결 관계를 찾아주는 기법이다. 은행의 FDS에서 이상한 거래를 탐지하거나, SNS의 친구 목록 중 실수로 추가한 친구를 찾아준다거나 하는 문제에 사용될 수 있다. 논문에는 아찔하게 많은 노테이션, 수학적 이론과 증명이 잔뜩 있다. 그것들은 모조리 스킵하고 핵심적인 이상 스코어링 공식을 이해하고, 이것을 실제 데이터에 적용하여 문제 해결에 응용해 볼 수 있는 방법을 정리해보자.
논문 링크: Outlier edge detection using random graph generation models and applications (2017)
Abstract
그래프와 관련하여 이상 Edge를 찾는 연구는 이상 Node를 찾는 것에 비하여 상대적으로 덜 중요하게 다루어졌다. 한 Edge를 둘러싼 주위의 그래프 구조를 살펴봄으로써 그 Edge의 이상 여부를 효율적으로 판단할 수 있는 알고리즘을 제안한다. 위 알고리즘은 단순히 이상 Edge를 찾는 것 이외에, 이상 Node를 찾는 문제나, 그래프 클러스터링이나 커뮤니티 탐지 성능 향상을 위한 전처리에도 유용하다.
Background
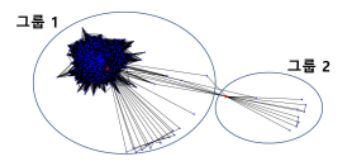
논문에서는 소셜 네트워크 그래프 클러스터링의 속성을 활용하여 Edge의 이상 정도를 구한다. 이상 정도는 엣지에 각각 연결된 두 노드가 포함된 두 그룹을 만들고, 두 그룹간의 실제 연결량과 기대 연결량의 차이를 통해 측정한다. 그리고 기대 연결량이라는 것을 추정하기 위해 random graph generation model을 사용한다.
Previous work
- Graph-based anomaly detection (2003)
- 그래프 안에서 자주 등장하지 않는 구조를 찾는다 (Minimum Description Length Technique)
- SCAN: A Structural Clustering Algorithm for Networks (2007)
- 상대적으로 그래프의 중심에서 멀고 연결된 엣지가 희소한 노드를 찾는다 (Searching strategy that share many common neighbors)
- On Community Outliers and their Efficient Detection in Information Networks (2010)
- 각 노드의 역할을 정의하고 역할이 없는(?) 친구를 찾는다
대부분의 연구는 이상 노드를 찾는 것에 집중됬고, 이상 엣지에 대한 선행 연구들도 결국은 이상 노드를 먼저 찾은 뒤 그것과 관련된 엣지를 찾는 식이었다. 혹은 노드간의 유사도를 기반으로 유실된 엣지를 찾는 detecting missing edges task도 생각해 볼 수 있는데, 아쉽게도 이 역시 이상 탐지에서는 큰 성능을 보이지 못했다.
Notation
| Notation | 의미 |
|---|---|
| G(V,E) | set of nodes V, set of edges E로 구성된 그래프 |
| a,b,c | 개별 노드는 영어 소문자로 표시 |
| ab | a,b를 연결된 edge (undirected) |
| N(a) | a와 연결된 이웃 노드들 (a 제외) |
| S(a) | N(a) + {a} |
| k(a) | number of Nodes in N(a) |
| n | number of Nodes in G(V,E) |
| m | number of Edges in G(V,E) |
| S(CN) | number of Nodes in N(a) & N(b) (CN:common neighbors) |
Method
Definition 1. G(ab) = G(V(ab), E(ab))
- V(ab): S(a) + S(b)
- E(ab): set of xy since x,y in V(ab)
G(ab)는 ab 엣지와 연결된 노드들과, 그 노드들간의 엣지로 구성된 그래프이다.
Definition 2. Score(ab) = m(ab) - e(ab)
- m(ab): N(a) ~ N(b)로 연결된 엣지 수
- e(ab): N(a) ~ N(b) 엣지의 기대값
Expected number of edges between two sets of nodes
- Erdős- Rényi random graph generation model
- G(n,m) model: n개 노드에서 랜덤하게 m개 엣지가 될 때까지 복원 생성 반복
- S,T 사전에 정의된 두 개의 노드 집합 (교집합 있을 수 있음)
- 두 그룹을 연결하는 엣지가 생성될 확률
![]()
- 따라서 m개 엣지에 대한 기댓값은 확률 * m
그래서 이거 데이터 어떻게 처리해서 알고리즘 적용하면 되는 거지?
Q: 노드 a, 노드 b를 연결한 edge(ab)는 얼마나 이상일까?
- 노드 a와 연결된 엣지가 있는 노드들: N(a)
- 노드 b와 연결된 엣지가 있는 노드들: N(b)
m(ab)
- m(ab)는 (1)과 (2)로 구성되어있다.
- 우선 (1)을 보자.
- P(ab)는 N(a)에서 b 노드를 뺀 노드들, R(ab)는 N(b)에서 P(ab)를 뺀 노드들.
- alpha(P(ab), R(ab))는 P(ab)의 노드들과 R(ab) 노드들이 연결된 Edge 수
- 다음 (2)를 보자.
- P(ba)는 N(b)에서 a 노드를 뺀 노드들, R(ba)는 N(a)에서 P(ba)를 뺀 노드들.
- alpha(P(ba), R(ba))는 P(ba)의 노드들과 R(ba) 노드들이 연결된 Edge 수
- 비슷해보이는 (1)과 (2)를 굳이 쪼개서 더하는 이유는 N(a)와 N(b)에 겹치는 노드가 있을 수 있기 때문
