Bootstrapping은
샘플에서 얻은 결과(point)를 분포에 대한 가정 없이 신뢰할 수 있는 구간(interval)으로 표현하기 위한 방법론이다.
예를 들어
성인 남성 키의 평균을 구하고 싶을 때, 전수조사를 할수는 없는 노릇이다.
Simple Random Sampling을 통해 무작위의 성인 남성들을 데리고 와 키를 재보자.
100명의 평균이 175라고 나왔을 때 "성인 남성 키의 평균은 175다"라고 말하기보다는,
"성인 남성 키의 평균은 95% 확률로 173과 177 사이에 있다"라고 표현하기 위한 하나의 방법론이다.
어떻게 하냐면
처음 데려온 100명의 성인 남성의 키에 대한 관측값을 반복해서 평균내는 것이다.
그런데 100명의 데이터를 온전히 한 번씩 사용하여 평균내는 것이 아니다.
100명의 데이터를 “복원추출”을 통해 새로운 100명의 데이터(새로운 샘플)로 만들어 평균내는 것이다.
그러면 누군가의 키는 반복해서 들어갔을 것이기 때문에 맨 처음 175라는 값과는 다른 결과가 나올 것이다.
이렇게 복원추출을 반복하여, 새로운 샘플들을 평균들을 모아보면 샘플링 분포를 얻을 수 있다.
그러면 이제 얻어진 분포를 사용해서 신뢰구간을 구하면 된다.
코드로 보면
1
2
3
4
5
6
7
8
9
import random
def random_float(low, high):
return random.random() * (high - low) + low
def random_height(size):
return [round(random_float(150,190),1) for i in range(size)]
sample_height = random_height(100)
150 ~ 190 사이의 성인 남성 100명의 키를 샘플로 얻었다고 생각해보자.
샘플 100명의 평균은 169.42라고 나온다. 그런데 이것을 신뢰구간으로 표현하고 싶다.
그리고 코드에서는 키가 uniform distribution을 따르도록 추출하였지만, 모른다고 가정하자.
1
2
def bootstrapping(data):
return [data[random.sample(range(len(data)),1)[0]] for i in range(len(data))]
함수는 들어온 데이터 사이즈만큼의 데이터를, 복원추출을 통해 생성한다.
bootstrapping 함수를 한 번 수행하여 새로 얻어진 샘플의 평균은 168.609라고 나왔다.
이제 이런 bootstrapping을 10,000 수행해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
import matplotlib.pyplot as plt
import numpy as np
sample_distribution = []
for i in range(10000):
sample_distribution.append(np.mean(bootstrapping(sample_height)))
plt.hist(sample_distribution, density=False, bins=100)
plt.ylabel('Count')
plt.xlabel('Mean Height');
display(plt.show())
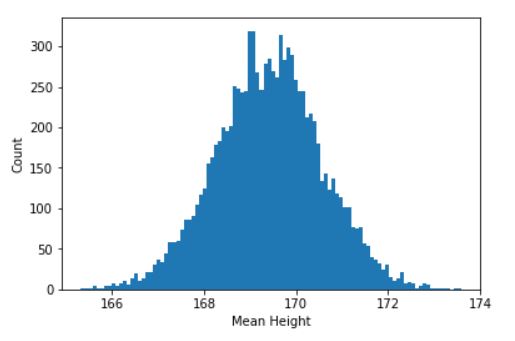
그림을 그려보면 아래와 같은 sampling distribution을 얻을 수 있다.
1
2
print(np.percentile(sample_distribution, 2.5)) # 167.1
print(np.percentile(sample_distribution, 97.5)) # 171.6
마지막으로, 샘플링 분포에서 상위 2.5% 하위 2.5%를 구하고 나면 우리는 95% 신뢰구간을 얻을 수 있다.
따라서, 성인 남성 키는 167.1 ~ 171.6 사이에 95% 신뢰 수준으로 존재한다고 말할 수 있다.
Bootstrapping의 장점은
(1) 우선 굉장히 간편하다. 딱히 공식이나 분포에 대한 이해나 지식이 필요 없다.
기계적으로 복원추출 샘플링을 반복하고, 상/하위 percentile을 구하기만 하면 된다.
(2) 또한 Bootstrapping은 분포에 대한 가정이 필요 없다.
모집단인 전체 성인 남성 키의 분포가가 uniform이든 normal이든 상관이 없다.
앞의 예제에서 100명의 샘플을 뽑을 때, unifrom 분포에서 샘플을 뽑았음에도 불구하고
중심극한정리에 의해 sampling distribution은 결국 정규 분포를 따르기 때문이다.
(3) 마지막으로, 평균이 아닌 다양한 statistic에 대해서도 같은 방식으로 신뢰 구간을 구할 수 있다.
예를들어 중위수나, 분산에 대해서도 완벽히 같은 방식으로 결론을 얻을 수 있다.
배경은
bootstrapping 방법을 처음 제안한 논문이라고 한다. 무려 21,600 번의 cited.
솔직히 무작정 읽어서는 사전 지식이 너무 많이 필요하여 잘 이해가 되지 않았다.
그러나 새로 알게 된 점은, 참조했던 자료들과 영상들이 bootstrapping 방법론의 일부였다는 것인데,
논문에서 제안된 샘플 분포의 측정 방법 중, 가장 대중적인 monte carlo approximation을 적용한 것이었다.
In machine learning
Bootstrapping의 컨셉을 머신러닝에 적용한 것이 Bagging이다.
주어진 n개의 데이터를, 여러번의 bootstrapping을 통해 m개의 샘플로 만든 뒤, m개의 모델을 학습한다.
그렇게 얻어진 m개의 모델 결과를 종합하여 최종 결과를 도출하는 방식의 모델링이다.
다양한 데이터를 학습하는 효과를 주기 때문에 모델의 성능을 높이고 오버피팅하지 않도록 도와준다.
참조